��Ŀ����
����Ŀ����֪������y��x2+��2n��1��x+n2��1��nΪ��������
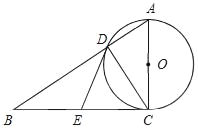
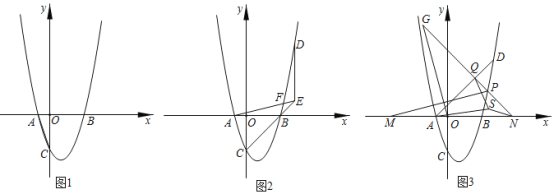
��1�����������߾�������ԭ�㣬���Ҷ����ڵ�������ʱ�����������Ӧ�ĺ�����ϵʽ��
��2����A�ǣ�1����ȷ������������λ��x���·������ڶԳ�������һ�����㣬��A��x���ƽ���ߣ�������������һ��D������AB��x����B��DC��x����C��
����BC��1ʱ�������ABCD���ܳ���
�����ʾ���ABCD���ܳ��Ƿ�������ֵ��������ڣ������������ֵ����ָ����ʱA������꣮��������ڣ���˵�����ɣ�
���𰸡���1��y��x2��3x����2��������ABCD���ܳ�Ϊ6������x��![]() ʱ������ABCD���ܳ�C���ֵΪ
ʱ������ABCD���ܳ�C���ֵΪ![]() ����ʱ��A������ΪA��
����ʱ��A������ΪA��![]() ��
��![]() ����
����
��������
��1����ԭ��������������ߵĽ���ʽ�У��������n��ֵ��Ȼ����������߶����ڵ����������������nֵ��ȥ�����ɵó�����Ķ��κ�������ʽ��
��2�����ȸ��������ߵĽ���ʽ�����������x����һ����E�����꣬���������ߺ;��εĶԳ��Կ�֪��OB�ij�������OE��BC�IJ��һ�룬�ɴ˿����OB�ij�����B������꣬Ȼ����������ߵĽ���ʽ�м������B�������꣬Ҳ�͵ó��˾���AB�ߵij���������������ε��ܳ�����˼·ͬ�ٿ����A�����꣨������꣬���������ߵĽ���ʽ��ʾ�����꣩��Ҳ���ܱ�ʾ��B������꣬���ɵó�OB�ij���ͬ�ٿɵó�BC�ij�����AB�ij�����A��������ľ���ֵ���ɴ˿ɵó�һ�����ھ����ܳ���A��������ĺ�����ϵʽ�����ݶ��κ��������ʿɵó������ܳ������ֵ����Ӧ��A�����꣮
��1������֪��������n2��1��0
��������̣���n1��1��n2����1
��n��1ʱ����y��x2+x���������ߵĶ��㲻�ڵ������ޣ�
��n����1ʱ����y��x2��3x���������ߵĶ����ڵ������ޣ�
������ĺ�����ϵʽΪy��x2��3x��
��2����y��x2��3x��
��y��0����x2��3x��0��
���x1��0��x2��3
����������x�����һ������ΪE��3��0��
�����Ķ���Ϊ![]() ���Գ���Ϊֱ��
���Գ���Ϊֱ��![]() �������λ����ͼ��ʾ��
�������λ����ͼ��ʾ��
�١�BC��1����֪OB��![]() ����3��1����1��
����3��1����1��
��B��1��0��
���A�ĺ�����x��1���ֵ�A��������y��x2��3x�ϣ�
���A��������y��12��3��1����2��
��AB��|y|��|��2|��2��
�����ABCD���ܳ�Ϊ��2��AB+BC����2����2+1����6��
�ڡߵ�A��������y��x2��3x�ϣ��ʿ���A�������Ϊ��x��x2��3x����
��B���������x��0����![]()
��BC��3��2x��A��x���·���
��x2��3x��0��
��AB��|x2��3x|��3x��x2
�����ABCD���ܳ�C��2[��3x��x2��+��3��2x��]��![]() ��
��
��a����2��0�������߿������£����κ��������ֵ��
�൱x��![]() ʱ������ABCD���ܳ�C���ֵΪ
ʱ������ABCD���ܳ�C���ֵΪ![]() ��
��
��ʱ��A������ΪA![]() ��
��

����Ŀ��ijУ������ǿ��ë������ƹ���������������������˶���ÿλͬѧ������ֻ��ѡ��һ�������˶����Ը�Уѧ�������ȡ![]() ���е��飬���ݵ�������������ͼ��������Ƶ���ֲ���������ͳ��ͼ��
���е��飬���ݵ�������������ͼ��������Ƶ���ֲ���������ͳ��ͼ��
�˶���Ŀ | Ƶ�� |
��� | 30 |
���� | a |
ƹ���� | 36 |
���� | b |
���� | 12 |
���������ͼ����Ϣ����������⣺
![]() Ƶ���ֲ����е�
Ƶ���ֲ����е�![]() ______��
______��![]() ______��
______��
![]() ������ͳ��ͼ�У������������ڵ����ε�Բ�Ľ�Ϊ______�ȣ�
������ͳ��ͼ�У������������ڵ����ε�Բ�Ľ�Ϊ______�ȣ�
![]() ȫУ�ж�����ѧ��ѡ��μ�ƹ�����˶���
ȫУ�ж�����ѧ��ѡ��μ�ƹ�����˶���

����Ŀ��Ϊ�˽���꼶ѧ��˫���յĿ����Ķ������ѧУ��������˸��꼶25��ѧ�����õ���һ���������ݣ���ͳ�Ʊ����£�
���꼶25��ѧ��˫���տ����Ķ�ʱ��ͳ�Ʊ�
�Ķ�ʱ�� | 1Сʱ | 2Сʱ | 3Сʱ | 4Сʱ | 5Сʱ | 6Сʱ |
���� | 3 | 4 | 6 | 3 | 2 |
��1��������Ķ�ʱ��Ϊ4Сʱ��������ռ�ٷֱȣ�
��2����ȷ�����������������ƽ������