题目内容
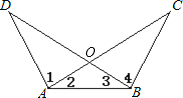
【题目】(2016.镇江)如图,AD、BC相交于点O,AD=BC,∠C=∠D=90°.
(1)若∠ABC=35°,求∠CAO的度数;
(2)求证:CO=DO

【答案】(1)20°;(2)见解析;
【解析】(1)根据HL证明Rt△ABC≌Rt△BAD;由全等的性质得∠BAD=∠ABC,根据直角三角形两直角互余可求∠BAC=55 ,从而可求出∠CAO的度数;
(2)利用全等三角形的性质可得∠BAD=∠ABC,BC=AD,从而可证求证CO=DO.
∵∠D=∠C=90°,
∴△ABC和△BAD都是Rt△,
在Rt△ABC和Rt△BAD中,
∵AD=BC,AB=BA,
∴Rt△ABC≌Rt△BAD(HL);
∴∠BAD=∠ABC=35°.
∵∠ABC=35°,
∴∠BAC=90-35=55,
∴∠CAO=55-35=20.
(2)证明:∵Rt△ABC≌Rt△BAD,
∴∠BAD=∠ABC,BC=AD,
∴AO=BO,
∴BC-BO=AD-AO,
∴CO=DO.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目