题目内容
如图,在⊙O中,∠ACB=∠BDC=60°,AC=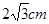 ,
,
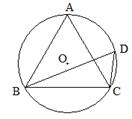
(1)判断△ABC的形状并证明你的结论;
(2)求⊙O的周长
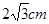 ,
,
(1)判断△ABC的形状并证明你的结论;
(2)求⊙O的周长
(1)见解析(1)4π
试题分析:利用圆周角定理可得∠BAC=∠CPB,∠ABC=∠APC,而∠APC=∠CPB=60°,所以∠BAC=∠ABC=60°,从而可判断△ABC的形状(2)由三角形内角和得∠ABC=60°,所以△ABC是等边三角形,作OE⊥AC,连接OA,由垂径定理得,AE=CE=
 AC=
AC= cm,再由余弦的概念求得半径OA的长,由圆的周长公式求得周长.
cm,再由余弦的概念求得半径OA的长,由圆的周长公式求得周长.解:(1)△ABC为等边三角形证明如下:
∵∠BAC和∠BDC都是弧BC所对的圆周角
∴∠BAC=∠BDC
∵∠ACB=∠BDC=60° ∴∠BAC =∠ACB =60°
∴△ABC为等边三角形……………………3分
(2)过O点作OE⊥AC于E点,连接OA
∵AC=
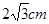 ∴AE=CE=
∴AE=CE=
∵△ABC为等边三角形
∴∠OAE=
 ∠BAC=30° 设OE=x,则OA=2x,
∠BAC=30° 设OE=x,则OA=2x,在Rt△OAE中,有
 ,解之得x=1
,解之得x=1∴OA=2 即⊙O的周长=2×2×π=4πcm
点评:本题考查了圆周角定理.同弧所对的圆周角相等,并且等于它所对的圆心角的一半.也考查了等边三角形的判定方法.本题利用了圆周角定理,等边三角形的判定和性质,垂径定理,余弦的概念,圆周长公式求解.

练习册系列答案
相关题目

 ,AB=
,AB= ,求AE的长.
,求AE的长.





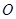 内有折线
内有折线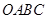 ,其中
,其中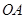 =8,,
=8,,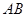 =12,∠
=12,∠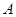 =∠
=∠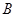 =60o,则
=60o,则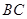 的长为( )。
的长为( )。