题目内容
【题目】在一个不透明的口袋中,放有三个标号分别为1,2,3的质地、大小都相同的小球.任意摸出一个小球,记为x,再从剩余的球中任意摸出一个小球,又记为y,得到点(x,y).
(1)用画树状图或列表等方法求出点(x,y)的所有可能情况;
(2)求点(x,y)在二次函数y=ax2﹣4ax+c(a≠0)图象的对称轴上的概率.
【答案】
(1)解:画树状图为:
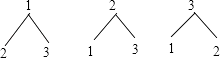
共有6种等可能的情况,分别为(1,2),(1,3),(2,1),(2,3),(3,1),(3,2);
(2)解:抛物线的对称轴为直线x=﹣ ![]() =2,
=2,
共有6种等可能的情况,其中点在对称轴上的情况有2种,分别为(2,1),(2,3),
∴P(点(x,y)在对称轴上)= ![]() =
= ![]() .
.
【解析】(1)分析球不放回的情况,根据“再从剩余的球中任意摸出一个小球”,画树状图分析可能的结果。
(2)根据抛物线的对称轴为直线x=-![]() ,先求出抛物线的对称轴,在根据(1)中所得到的点求出概率。
,先求出抛物线的对称轴,在根据(1)中所得到的点求出概率。
【考点精析】本题主要考查了二次函数的性质和列表法与树状图法的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小;当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率才能正确解答此题.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案
相关题目




