题目内容
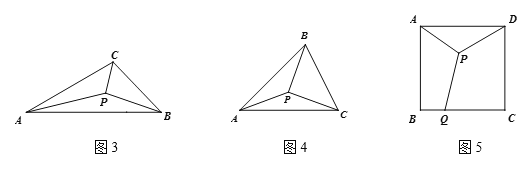
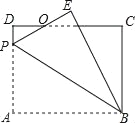
【题目】如图,四边形ABCD中,AB=AD,AB⊥BC,AD⊥CD,P是对角线AC上一点,

求证:PB=PD.
【答案】证明见解析.
【解析】
试题易证△ABC和△ADC均为直角三角形,即可证明RT△ABC≌RT△ADC,可得∠BAC=∠DAC,即可证明△BAP≌△DAP,可得PB=PD,即可解题.
试题解析:
∵AB=AD,AB⊥BC,AD⊥CD,AC=AC
∴Rt△ABC≌Rt△ADC(HL)
∴CB=CD(全等三角形的对应边相等)
∴AC平分∠BAD(在一个角的内部, 到角的两边距离相等的点在这个角的平分线上)
∵AB=AD,∠BAP=∠ADP,AP=AP
∴△APB≌△APD.(SAS)
∴PB=PD. (全等三角形的对应边相等)

练习册系列答案
相关题目