Question

【题目】如图，直线AB与CD相交于点O， ．

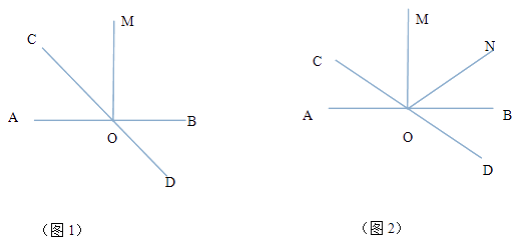
（1）如图1，若OC平分 ，求 的度数；
（2）如图2，若 ，且OM平分 ，求 的度数．

Answer 1

【答案】
（1）解：∵∠AOM=90°，OC平分∠AOM
∴∠AOC= ∠AOM=45°
∵∠AOC+∠AOD=180°
∴∠AOD=180°－∠AOC=180°－45°=135°
（2）解：∵∠BOC=4∠NOB
∴设∠NOB=x°，∠BOC=4x°
∴∠CON=∠COB-∠BON=4x°-x°=3x°
∵OM平分∠CON
∴∠COM=∠MON= ∠CON= x°
∵
解得：x=36
∴∠MON= x°= ×36°=54°
即∠MON的度数为54°
【解析】（1）根据OC平分 ∠AOM求出∠AOC的度数，再根据邻补角的定义求出∠AOD的度数即可。
（2）设∠NOB=x°，利用∠BOC=4∠NOB，表示出∠BOC的度数，从而得出∠CON的度数，再根据角平分线的定义得出∠COM=∠MON，再根据∠NOB+∠MON=90°，建立方程求解，再求出∠MON的度数。