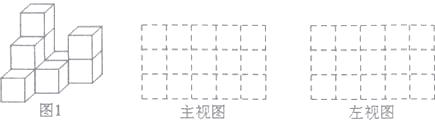
题目内容
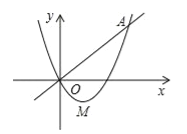
【题目】如图,在平面直角坐标系xOy中,一次函数y=x与二次函数![]() 的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
的图象相交于O、A两点,点A(3,3),点M为抛物线的顶点.
(1)求二次函数的表达式;
(2)长度为![]() 的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
的线段PQ在线段OA(不包括端点)上滑动,分别过点P、Q作x轴的垂线交抛物线于点P1、Q1,求四边形PQQ1P1面积的最大值;
(3)直线OA上是否存在点E,使得点E关于直线MA的对称点F满足S△AOF=S△AOM?若存在,求出点E的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)E(
;(3)E(![]() ,
,![]() ).
).
【解析】(1)把点A(3,3)代入![]() 中,得:3=9+3b,解得:b=﹣2,∴二次函数的表达式为
中,得:3=9+3b,解得:b=﹣2,∴二次函数的表达式为![]() .
.
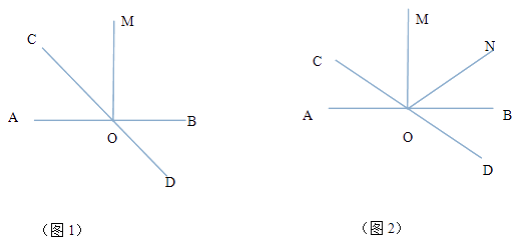
(2)设点P在点Q的左下方,过点P作PE⊥QQ1于点E,如图1所示.
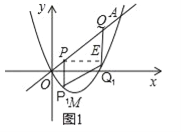
∵PE⊥QQ1,QQ1⊥x轴,∴PE∥x轴,∵直线OA的解析式为y=kx,∴∠QPE=45°,∴PE=![]() PQ=2.
PQ=2.
设点P(m,m)(0<m<1),则Q(m+2,m+2),P1(m,![]() ),Q1(m+2,
),Q1(m+2,![]() ),∴PP1=
),∴PP1=![]() ,QQ1=
,QQ1=![]() ,∴
,∴![]() =
=![]() (PP1+QQ1)PE=
(PP1+QQ1)PE=![]() =
=![]() ,∴当m=
,∴当m=![]() 时,
时,![]() 取最大值,最大值为
取最大值,最大值为![]() .
.
(3)存在.
如图2中,点E的对称点为F,EF与AM交于点G,连接OM、MF、AF、OF.
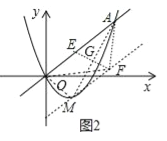
∵S△AOF=S△AOM,∴MF∥OA,∵EG=GF,![]() ,∴AG=GM,∵M(1,﹣1),A(3,3),∴点G(2,1),∵直线AM解析式为y=2x﹣3,∴线段AM的中垂线EF的解析式为
,∴AG=GM,∵M(1,﹣1),A(3,3),∴点G(2,1),∵直线AM解析式为y=2x﹣3,∴线段AM的中垂线EF的解析式为![]() ,由
,由 ,解得
,解得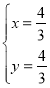 ,∴点E坐标为(
,∴点E坐标为(![]() ,
,![]() ).
).

练习册系列答案
相关题目