题目内容
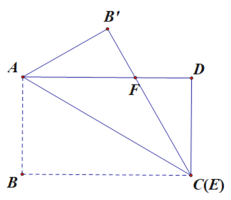
【题目】如图,在矩形纸片ABCD中,已知AB=2,BC=![]() ,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.
,点E在边CD上移动,连接AE,将多边形ABCE沿直线AE翻折,得到多边形AB′C′E,点B、C的对应点分别为点B′、C′.
(1)当点E与点C重合时,求DF的长;
(2)若B′C′分别交边AD,CD于点F,G,且∠DAE=22.5°,求△DFG的面积;
(3)如果点M为CD的中点,那么在点E从点C移动到点D的过程中,求C′M的最小值.

【答案】(1) DF=![]() ;(2)
;(2) ![]() ;(3) 4-
;(3) 4-![]()
【解析】
(1)根据特殊直角三角形求出∠FCD=30°, 在Rt△CDF中利用三角函数即可求解,
(2)由旋转的性质证明△DFG,△EG C′是等腰直角三角形,求出DF的长即可解题,
(3)找到C′,在Rt△ADM中和Rt△A B′C′中,勾股定理求出AM和A C′的长即可解题.
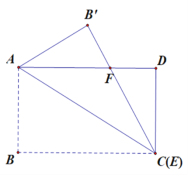
解:(1)如下图,
∵四边形ABCD是矩形, AB=2,BC=![]() ,
,
∴易证∠ACB=30°,
由旋转可知∠ACF=30°,
∴∠FCD=30°,
在Rt△CDF中,DF=tan30°CD=![]() ,
,
(2)如下图,由旋转可知,AB= AB′=2,BC= B′C′=![]() ,
,
∵∠DAE=22.5°,
∴∠BAE=67.5°,∠B′AF=45°,
∴△DFG,△EG C′是等腰直角三角形,
∴AF=2![]() ,DF=
,DF=![]() -2
-2![]() ,
,
S△DFG=![]() DF2=
DF2=![]() ,
,
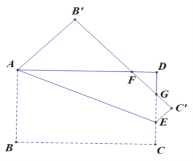
(3)连接AM并延长到点C′,连接A C′,M C′即为所求,见下图,
∵M为CD的中点,
∴DM=1,
在Rt△ADM中,AM=![]() ,
,
在Rt△A B′C′中, A C′=4,
∴M C′=4-![]() .
.

练习册系列答案
相关题目