题目内容
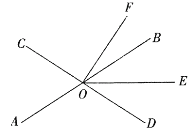
【题目】如图,直线![]() 、
、![]() 相交于点
相交于点![]() ,
,![]() 平分
平分![]() .
.
(1)若![]() ,求
,求![]() 的度数;
的度数;
(2)若![]() 平分
平分![]() ,∠BOF=12°,若设∠BOE=x°.
,∠BOF=12°,若设∠BOE=x°.
①则![]() = . (用含
= . (用含![]() 的代数式表示)
的代数式表示)
②求![]() 的度数.
的度数.
【答案】(1)55°(2)①![]() ②104°
②104°
【解析】
(1)由对顶角的性质可知∠BOD=70°,从而可求得∠FOB=20°,由角平分线的定义可知∠BOE=![]() ∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;
∠BOD,最后根据∠EOF=∠BOE+∠FOB求解即可;
(2)①先证明∠AOE=∠COE=x,然后由角平分线的定义可知∠FOE=![]() x;
x;
②∠BOE=∠FOE-∠FOB可知∠BOE=![]() x-15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.
x-15°,最后根据∠BOE+∠AOE=180°列出方程可求得x的值,从而可求得∠AOC的度数.
(1)由对顶角相等可知:∠BOD=∠AOC=70°,
∵∠FOB=∠DOF-∠BOD,
∴∠FOB=90°-70°=20°,
∵OE平分∠BOD,
∴∠BOE=![]() ∠BOD=
∠BOD=![]() ×70°=35°,
×70°=35°,
∴∠EOF=∠FOB+∠BOE=35°+20°=55°,
(2)①∵OE平分∠BOD,∠BOE=x°,
∴∠DOE=∠BOE=x,
∵∠COE+∠DOE=180o,
∴∠COE=180o-xo,
∵OF平分∠COE,
∴∠FOE=![]() ∠COE=
∠COE=![]() ,
,
故答案为:![]() ;
;
②∵∠BOE=∠FOE-∠FOB,
∴∠BOE=![]() x-12°,
x-12°,
∵∠BOE+∠AOE=180°,
∴![]() x-12°+x=180°,
x-12°+x=180°,
解得:x=128°,
∴∠AOC=2∠BOE=2×(180°-128°)=104°.

【题目】阅读可以增进人们的知识,也能陶冶人们的情操.我们要多阅读有营养的书.某校对学生的课外阅读时间进行了抽样调查,将收集的数据分成A,B,C,D,E五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
阅读时间分组统计表
组别 | 阅读时间x(h) | 人数 |
A | 0≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | b |
D | 30≤x<40 | 140 |
E | x≥40 | c |
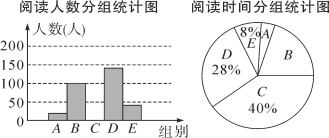
请结合以上信息解答下列问题:
(1)求a,b,c的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.