��Ŀ����
����Ŀ����������֤����
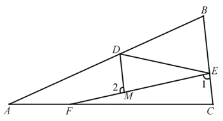
��֪����ͼ���� D��E��F �ֱ����߶� AB��BC��AC �ϣ����� DE��EF��DM ƽ�֡�ADE �� EF �ڵ� M����1+��2=180���� ��֤����B =��BED��
֤�����ߡ�1+��2=180������֪����
���ߡ�1+��BEM=180����ƽ�Ƕ��壩��
���2=��BEM�� ����
��DM�� �� ����
���ADM =��B�� ����
��MDE =��BED�� ����
����DM ƽ����ADE (��֪)��
���ADM =��MDE (��ƽ���߶���)��
���B =��BED�� ����
���𰸡�������
��������
����ƽ���ߵ��ж������ʡ�ͬ�ǻ�ȽǵIJ���������ɵã�
֤�����ߡ�1+��2=180������֪����
�֡ߡ�1+��BEM=180����ƽ�Ƕ��壩��
���2=��BEM��ͬ�ǵIJ�����ȣ���
��DM��BC��ͬλ�������ֱ��ƽ�У���
���ADM=��B����ֱ��ƽ��ͬλ����ȣ���
��MDE=��BED����ֱ��ƽ���ڴ�����ȣ���
�֡�DMƽ�֡�ADE����֪����
���ADM=��MDE����ƽ���߶��壩��
���B=��BED��������������

��ϰ��ϵ�д�
�����Ŀ




