题目内容
【题目】记Sn＝a1+a2+…+an，令Tn＝
，称Tn为a1，a2，…，an这列数的“神秘数”．已知a1，a2，…，a500的“神秘数”为1503，那么6，a1，a2，…，a500的“神秘数”为（ ）
A.1504B.1506C.1508D.1510
【答案】B
【解析】
先根据已知求出T500的值，再设出新的理想数为Tx，列出式子，把得数代入，即可求出结果．
∵Tn＝
，
∴n×Tn＝（S1+S2+…+Sn），
∵a1，a2，…，a500的“神秘数”为1503，
∴T500＝1503
设6，a1，a2，…，a500的“神秘数”为Tx，
则501×Tx＝6×501+500×T500，
∴Tx＝（6×501+500×T500）÷501
＝
＝6+500×3
＝1506，
故选B．
练习册系列答案
相关题目
【题目】小张同学尝试运用课堂上学到的方法，自主研究函数
的图像与性质.下面是小张同学在研究过程中遇到的几个问题，现由你来完成：
（1）函数y=
的定义域是 ；
（2）下表列出了
与
的几组对应值：
| … |
|
|
|
|
|
|
| 1 |
|
| … |
| … |
|
|
|
|
| 4 |
| 1 |
|
| … |
表中
的值是 ；
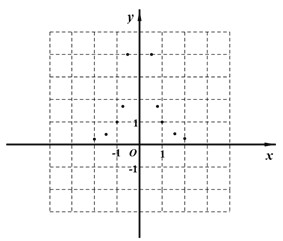
（3）如图，在平面直角坐标系
中，描出以表中各组对应值为坐标的点，试由描出的点画出该函数的图像；
（4）结合函数的图像，写出这个函数的性质： .（只需写一个）
