题目内容
如图,在梯形 中
中 ,
, ,已知
,已知 ,点
,点 为
为 边上的动点,连接
边上的动点,连接 ,以
,以 为圆心,
为圆心, 为半径的⊙
为半径的⊙ 分别交射线
分别交射线 于点
于点 ,交射线
,交射线 于点
于点 ,交射线
,交射线 于
于 ,连接
,连接 .
.

(1)求 的长.
的长.
(2)当 时,求
时,求 的长.
的长.
(3)在点 的运动过程中,
的运动过程中,
①当 时,求⊙
时,求⊙ 的半径.
的半径.
②当 时,求⊙
时,求⊙ 的半径(直接写出答案).
的半径(直接写出答案).
 中
中 ,
, ,已知
,已知 ,点
,点 为
为 边上的动点,连接
边上的动点,连接 ,以
,以 为圆心,
为圆心, 为半径的⊙
为半径的⊙ 分别交射线
分别交射线 于点
于点 ,交射线
,交射线 于点
于点 ,交射线
,交射线 于
于 ,连接
,连接 .
.
(1)求
 的长.
的长.(2)当
 时,求
时,求 的长.
的长.(3)在点
 的运动过程中,
的运动过程中,①当
 时,求⊙
时,求⊙ 的半径.
的半径.②当
 时,求⊙
时,求⊙ 的半径(直接写出答案).
的半径(直接写出答案).(1)4;(2)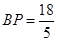 ;(3)①
;(3)①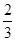 ;②
;② 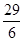
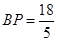 ;(3)①
;(3)①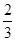 ;②
;② 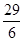
试题分析:(1)过点A作AE⊥BC,在Rt△ABE中,由AB=5,
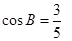 ,可得BE=3,在由勾股定理求得AE的长,证得四边形
,可得BE=3,在由勾股定理求得AE的长,证得四边形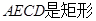 ,即可求得结果;
,即可求得结果;(2)由CD⊥BC,BC=6即可求得AD的长,当
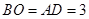 时,在⊙O中,过点O作OH⊥AB,则BH=HP,先由∠B的余弦函数求得BH的长,即可得到
时,在⊙O中,过点O作OH⊥AB,则BH=HP,先由∠B的余弦函数求得BH的长,即可得到 的长;
的长;(3)①设⊙
 的半径为r,当
的半径为r,当 时,有
时,有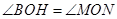 ,根据正切函数即可列方程求得⊙
,根据正切函数即可列方程求得⊙ 的半径;②解法同①.
的半径;②解法同①.(1)过点A作AE⊥BC
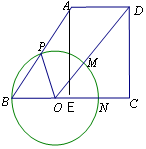
在Rt△ABE中,由AB=5,
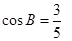 ,得BE=3,由勾股定理得
,得BE=3,由勾股定理得
易得四边形
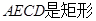
∴
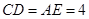 ;
;(2)∵CD⊥BC,BC=6
∴

当
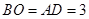 时,在⊙O中,过点O作OH⊥AB,则BH=HP,
时,在⊙O中,过点O作OH⊥AB,则BH=HP,∵
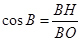
∴
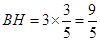
∴
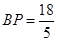 ;
;(3)①设⊙
 的半径为r
的半径为r当
 时,
时,有
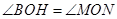
此时
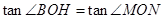
∴
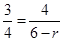
∴
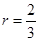
即⊙
 的半径为
的半径为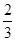
②⊙
 的半径为
的半径为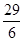
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目


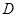 为
为 上一点,点
上一点,点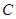 在直径
在直径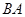 的延长线上,
的延长线上,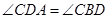 .
.
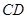 是
是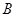 作
作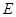 ,若BC=4,tan∠ABD=
,若BC=4,tan∠ABD=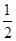 求
求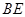 的长.
的长.

 cm2.
cm2.