题目内容
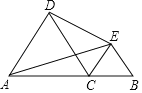
【题目】如图,点C为线段AB上一点,且CB=1,分别以AC、BC为边,在AB的同一侧作等边△ACD和等边△CBE,连接DE,AE,∠CDE=30°,则△ADE的面积为_____.
【答案】![]()
【解析】
由等边三角形的性质得出CE=CB=1,AD=CD,∠DCA=∠ECB=∠ADC=60°,由平角的定义得出∠DCE=60°,由三角形内角和定理得出∠CED=90°,由含30°角的直角三角形的性质得出CE=![]() CD,即AD=CD=2CE=2,DE=CDsin60°=2×
CD,即AD=CD=2CE=2,DE=CDsin60°=2×![]() =
=![]() ,∠ADE=∠ADC+∠CDE=90°,则S△ADE=
,∠ADE=∠ADC+∠CDE=90°,则S△ADE=![]() ADDE,即可得出结果.
ADDE,即可得出结果.
解:∵△ACD和△CBE都是等边三角形,
∴CE=CB=1,AD=CD,∠DCA=∠ECB=∠ADC=60°,
∴∠DCE=180°﹣∠DCA﹣∠ECB=180°﹣60°﹣60°=60°,
∵∠CDE=30°,
∴∠CED=180°﹣∠CDE﹣∠DCE=180°﹣30°﹣60°=90°,
∴CE=![]() CD,即AD=CD=2CE=2,
CD,即AD=CD=2CE=2,
DE=CDsin60°=2×![]() =
=![]() ,
,
∠ADE=∠ADC+∠CDE=60°+30°=90°,
∴S△ADE=![]() ADDE=
ADDE=![]() ×2×
×2×![]() =
=![]() ,
,
故答案为:![]() .
.

 金博士一点全通系列答案
金博士一点全通系列答案【题目】二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣1 | ﹣ | ﹣2 | ﹣ | … |
根据表格中的信息,完成下列各题:
(1)当x=3时,y=________;
(2)当x=_____时,y有最________值为________;
(3)若点A(x1,y1)、B(x2,y2)是该二次函数图象上的两点,且﹣1<x1<0,1<x2<2,试比较两函数值的大小:y1________y2 ;
(4)若自变量x的取值范围是0≤x≤5,则函数值y的取值范围是________.