题目内容
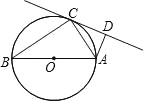
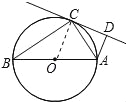
【题目】如图,AB是⊙O的直径,C是⊙O上一点,∠ACD=∠B,AD⊥CD.
(1)求证:CD是⊙O的切线;
(2)若AD=1,OA=2,求AC的值.
【答案】(1)证明见解析;(2)2.
【解析】
试题分析:(1)连接OC,易知∠ACB=90°. ∠B=∠BCO,可推出∠OCD=90°,可得出结论;(2)可证△ACB∽△ADC,利用对应边成比例可求得AC的值.
试题解析:(1)证明:连接OC,∵AB是⊙O直径,∴∠ACB=90°,∵OB=OC,∴∠B=∠BCO,又∵∠ACD=∠B,
∴∠OCD=∠OCA+∠ACD=∠OCA+∠BCO=∠ACB=90°,即OC⊥CD,∴CD是⊙O的切线;(2)解:∵AD⊥CD,
∴∠ADC=∠ACB=90°,又∵∠ACD=∠B,∴△ACB∽△ADC,∴![]() ,∴AC2=ADAB=1×4=4,∴AC=2.
,∴AC2=ADAB=1×4=4,∴AC=2.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目