题目内容
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别为AB , AC边上的中点,连接DE , 将△ADE绕点E旋转180°得到△CFE , 连接AF , AC . 求证:四边形ADCF是菱形;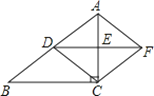
【答案】解答:证明:∵将△ADE绕点E旋转180°得到△CFE ,
∴AE=CE , DE=EF ,
∴四边形ADCF是平行四边形,
∵D、E分别为AB , AC边上的中点,
∴DE是△ABC的中位线,
∴DE∥BC ,
∵∠ACB=90°,
∴∠AED=90°,
∴DF⊥AC ,
∴四边形ADCF是菱形.
【解析】根据旋转可得AE=CE , DE=EF , 可判定四边形ADCF是平行四边形,然后证明DF⊥AC , 可得四边形ADCF是菱形.
【考点精析】通过灵活运用三角形中位线定理和菱形的判定方法,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形即可以解答此题.

练习册系列答案
 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案
相关题目