题目内容
如图,在正方形ABCD中,AD=8,点E是边CD上(不包括端点)的动点,AE的中垂线FG分别
交AD、AE、BC于点F、H、K,交AB的延长线于点G。
(1)设DE=m,![]() =t,用含m的代数式表示t;
=t,用含m的代数式表示t;
(2)当t=![]() 时,求BG的长。
时,求BG的长。

答案:
解析:
解析:
| (1)过点H作MN//CD分别交AD、BC于点M、N。
∵ FG是AE的中线,∴ HA=HE。∴ MA=MD。 ∴ MH是△ADE的中位线。 ∴MH= ∵ 四边形ABCD是正方形, ∴ 四边形ABNM是矩形。 ∴ MN=AB=AD=8。 ∴ HN=MN-MH=8- ∵ AD//BC,∴ (2)过点H作HT⊥AB于点T, ∵t= ∴MH= HN=8- ∴ AT=MH=2。TB=HN=6。∵ ∠AHG=90°。 ∴ HT2=AT·TG。又∵ HT=AM=4, ∴ 16=2TG。∴ TG=8。 ∴ BG=TG-TB=8-6=2。
|

练习册系列答案
相关题目
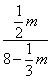
 如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比.
如图:在正方形网格上有△ABC,△DEF,说明这两个三角形相似,并求出它们的相似比. ,交BC于点E.
,交BC于点E. 23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
23、如图,在Rt△ABC中,∠BAC=90°,AD=CD,点E是边AC的中点,连接DE,DE的延长线与边BC相交于点F,AG∥BC,交DE于点G,连接AF、CG.
 如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6
如图,在Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O,连接OC,已知AC=5,OC=6