题目内容
【题目】已知△ABC,以AC为边在△ABC外作等腰△ACD,其中AC=AD.
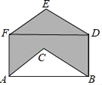
(1)如图1,若∠DAC=2∠ABC,AC=BC,四边形ABCD是平行四边形,则∠ABC=____.45°;
(2)如图2,若∠ABC=30°,△ACD是等边三角形,AB=3,BC=4.求BD的长;
(3)如图3,若∠ABC=30°,∠ACD=45°,AC=2,B、D之间距离是否有最大值?如有求出最大值;若不存在,说明理由.
【答案】(1)45°;(2)BD=5;(3)当B、O、D共线时,BD的值最大,最大值为2+![]() .
.
【解析】
(1)由AC=AD得∠D=∠ACD,由平行四边形的性质得∠D=∠ABC,在△ACD中,由内角和定理求解;
(2)如图2,在△ABC外作等边△BAE,连接CE,利用旋转法证明△EAC≌△BAD,可证∠EBC=90°,BE=AB=3,在Rt△BCE中,由勾股定理求CE,由三角形全等得BD=CE;
(3)如图3中,在△ACD的外部作等边三角形△ACO,以O为圆心OA为半径作⊙O.首先说明点B在⊙O上运动,当B、O、D共线时,BD的值最大,求出OD即可解决问题;
(1)解:(1)如图1中,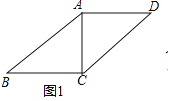
∵AD∥BC,
∴∠DAC=∠BCA.∠DAB+∠ABC=180°.
∵AC=BC,
∴∠ABC=∠BAC.
∵∠DAC=2∠ABC,
∴2∠ABC+2∠ABC=180°,
∴∠ABC=45°
故答案为:45;
(2)如图2,以AB为边在△ABC外作等边三角形△ABE,连接CE.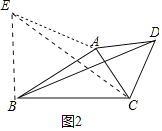
∵△ACD是等边三角形,
∴AD=AC,∠DAC=60°.
∵∠BAE=60°,
∴∠DAC+∠BAC=∠BAE+∠BAC.
即∠EAC=∠BAD
∴△EAC≌△BAD.
∴EC=BD.
∵△AEB是等边三角形,
∴∠EBA=60°,EB=3,
∵∠ABC=30°,
∴∠EBC=90°.
∵∠EBC=90°,EB=3,BC=4,
∴EC=5.
∴BD=5.
(3)如图3中,在△ACD的外部作等边三角形△ACO,以O为圆心OA为半径作⊙O.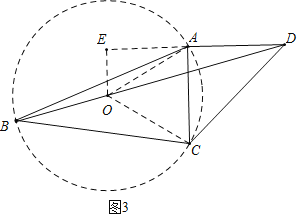
∵∠ABC=![]() ∠AOC=30°,
∠AOC=30°,
∴点B在⊙O上运动,
作OE⊥DA交DA的延长线于E.
在Rt△AOE中,OA=AC=2,∠EAO=30°,
∴OE=![]() OA=1,AE=
OA=1,AE=![]() ,
,
在Rt△ODE中,DE=AE+AD=2+![]() ,
,
∴DO=![]() =
=![]() ,
,
当B、O、D共线时,BD的值最大,最大值为OB+OD=2+![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某小组在学校组织的研究性学习活动中了解所居住的小区500户居民的人均收入情况,从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了如下的频数分布表和频数分布直方图,根据以上提供的信息,解答下列问题:
分组 | 频数 | 百分比 |
600≤x<800 | 2 | 5% |
800≤x<1000 | 6 | 15% |
1000≤x<1200 | 45% | |
9 | 22.5% | |
1600≤x<1800 | 2 | |
合计 | 40 | 100% |
(1)补全频数分布表.
(2)补全频数分布直方图.

(3)请你估计该居民小区家庭人均收入属于中等收入(1000≤x<1600)的大约有多少户?