Question

已知：抛物线y=-x²+bx+c过点A（-1，0）、B（-2，-5），与y轴交于点C，顶点为D．
（1）求该抛物线的解析式；
（2）某直线过点A（-1，0），且与抛物线只有一个交点，求此直线的解析式；
（3）直线l过点C，且l∥x轴，E为l上一个动点，EF⊥x轴于F．求使DE+EF+BF的和为最小值的E、F两点的坐标，并直接写出DE+EF+BF的最小值．

Answer 1

分析：（1）将A（-1，0）、B（-2，-5）两点坐标代入y=-x²+bx+c即可求得该抛物线的解析式；
（2）设直线解析式为y=kx+m，要想使直线与抛物线只有一个交点，方程x²+（k-2）x+k-3=0有两个相等的实数根，解方程即可得出直线的解析式；
（3）先求出D点坐标，将D向下平移3个单位得D′点，求出直线BD′的解析式，便可求出F点坐标，进而求得E点坐标，可得DE+EF+BF的最小值是3+3

5

．

解答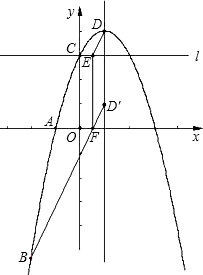：解：（1）根据题意，得：

-1-b+c=0 -4-2b+c=-5

，
解得：

b=2 c=3

，
∴所求抛物线的解析式为y=-x²+2x+3；

（2）①若所求直线与y轴相交，设其解析式为y=kx+m（k≠0），
∵直线过A（-1，0），
∴m=k，
∴y=kx+k，
∵直线y=kx+k与抛物线y=-x²+2x+3只有一个交点，
∴方程kx+k=-x²+2x+3有两个相等的实数根，
即方程x²+（k-2）x+k-3=0有两个相等的实数根，
∴△=k²-8k+16=0，
∴k₁=k₂=4，
∴直线的解析式为y=4x+4，
②若所求直线与y轴平行，所求直线为x=-1，
综上所述，所求直线的解析式为y=4x+4或x=-1；

（3）抛物线y=-x²+2x+3的顶点坐标为D（1，4），与y轴交点C（0，3）．
把点D（1，4）向下平移3个单位，得到D′（1，1），
连接BD′交x轴于点F，
过点F作FE⊥直线l于E，则E、F两点为所求．
设直线BD′的解析式为：y=ax+n（a≠0）
则

-2a+n=-5 a+n=1

，
解得：

a=2 n=-1

，
∴直线BD′的解析式为：y=2x-1，
∴直线BD′与x轴的交点F（

1

2

，0），
∵EF⊥x轴，EF=3，
∴E（

1

2

，3），
∴DE+EF+BF的最小值是3+3

5

．

点评：本题是二次函数的综合题，其中涉及到的知识点有抛物线的公式的求法和方程有相等实数根的解及动点问题等知识点，是各地中考的热点和难点，解题时注意数形结合数学思想的运用，同学们要加强训练，属于中档题．