题目内容
如图，把矩形ABCD对折，折痕为MN，矩形DMNC与矩形ABCD相似，已知
，求AB的长．
，求AB的长．1
试题分析：先根据
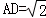求出MD的长，再根据矩形DMNC与矩形ABCD相似得出矩形对应边的比例式，求出AB的长即可．解：∵AD=
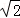，∴MD=NC=
，∵矩形DMNC与矩形ABCD相似，
∴
=
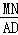，即
=
，∴AB=1．
点评：本题考查的是相似多边形的性质，即相似多边形的对应边成比例．
练习册系列答案
百年学典课时学练测系列答案
相关题目
试题分析：先根据
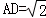求出MD的长，再根据矩形DMNC与矩形ABCD相似得出矩形对应边的比例式，求出AB的长即可．解：∵AD=
，∴MD=NC=
，∵矩形DMNC与矩形ABCD相似，
∴
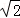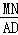=，即=，∴AB=1．
点评：本题考查的是相似多边形的性质，即相似多边形的对应边成比例．
百年学典课时学练测系列答案
= ．
= ；
的等边三角形，△ABC∽△ADE，AB=2AD，∠BAD=45°，AC与DE相交于点F，则△AEF的面积等于 _________ （结果保留根号）．
，又设V甲、V乙分别表示这两个正方体的体积，则
．
，那么它们的面积之比为 ．