题目内容
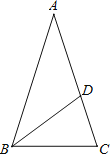
【题目】如图,AB是⊙O的直径,BC是⊙O的切线,D是⊙O上一点,且AD∥OC
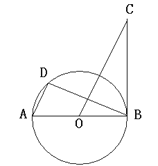
(1)求证:△ADB∽△OBC;
(2)若AB=2,BC=![]() ,求AD的长(结果保留根号).
,求AD的长(结果保留根号).
【答案】(1)∵AD∥OC,
∴∠A=∠COB,
∵AB是⊙O的直径,BC是⊙O的切线,
∴∠D=90°,∠CBO=90°,
即∠A=∠COB,∠D=∠CBO,
∴△ADB∽△OBC;
(2)AD=![]()
【解析】
试题(1)由AD∥OC可得∠A=∠COB,再根据AB是⊙O的直径,BC是⊙O的切线可得∠D=∠CBO=90°,即可证得结论;
(2)根据相似三角形的对应边成比例即可求得结果.
(1)∵AD∥OC,
∴∠A=∠COB,
∵AB是⊙O的直径,BC是⊙O的切线,
∴∠D=90°,∠CBO=90°,
即∠A=∠COB,∠D=∠CBO,
∴△ADB∽△OBC;
(2)![]()
∴![]()
∵△ADB∽△OBC,
![]()
![]()
解得![]()

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了鼓励居民节约用水,某市自来水公司按如下方式对每户月用水量进行计算:当用水量不超过![]() 吨时,每吨的收费标准相同,当用水量超过
吨时,每吨的收费标准相同,当用水量超过![]() 吨时,超出
吨时,超出![]() 吨的部分每吨的收费标准也相同,下表是小明家
吨的部分每吨的收费标准也相同,下表是小明家![]() 月份用水量和交费情况:
月份用水量和交费情况:
月份 |
|
|
|
|
用水量(吨) |
|
|
|
|
费用(元) |
|
|
|
|
请根据表格中提供的信息,回答以下问题:
(1)若小明家![]() 月份用水量为
月份用水量为![]() 吨,则应缴水费________元;
吨,则应缴水费________元;
(2)若某户某月用了![]() 吨水(
吨水(![]() ),应付水费________元;
),应付水费________元;
(3)若小明家![]() 月份交纳水费
月份交纳水费![]() 元,则小明家
元,则小明家![]() 月份用水多少吨?
月份用水多少吨?