题目内容
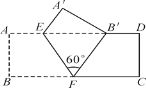
【题目】如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=1,DE=3,∠EFB′=60°,则矩形ABCD的面积是( )
A.4B.8C.3![]() D.4
D.4![]()
【答案】D
【解析】
由折叠可得AE=A'E=1,∠EFB=∠EFB'=60°,根据平行线性质可得∠A'EF=120°,∠B'EF=60°,解直角三角形A'E'B'可得A'B'的长度,则可求矩形ABCD面积.
∵把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,
∴∠BFE=∠EFB'=60°,AB=A'B'∠A=∠A'=90°,AE=A'E=2,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠DEF=∠EFB=60°,
∵A'E∥B'F,
∴∠A'EF+∠EFB'=180°,
∴∠A'EF=120°,
∴∠A'EB'=60°且∠A'=90°,
∴∠A'B'E=30°,且A'E=1,
∴B'E=2,A'B'=![]() =AB,
=AB,
∵AE=1,DE=3,
∴AD=4,
∴S矩形ABCD=AB×AD=4×![]() =4
=4![]() ,
,
故选:D.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目