题目内容
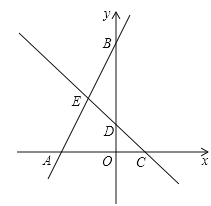
【题目】如图,在平面直角坐标系中,点O为坐标原点,直线y=﹣x+b与坐标轴交于C,D两点,直线AB与坐标轴交于A,B两点,线段OA,OC的长是方程![]() 的两个根(OA>OC).
的两个根(OA>OC).
(1)求点A,C的坐标;
(2)直线AB与直线CD交于点E,若点E是线段AB的中点,反比例函数![]() (k≠0)的图象的一个分支经过点E,求k的值;
(k≠0)的图象的一个分支经过点E,求k的值;
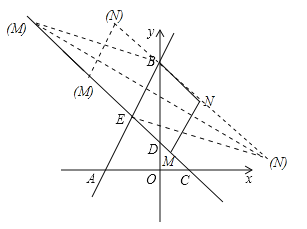
(3)在(2)的条件下,点M在直线CD上,坐标平面内是否存在点N,使以点B,E,M,N为顶点的四边形是菱形?若存在,请直接写出满足条件的点N的坐标;若不存在,请说明理由.
【答案】(1)A(﹣2,0),C(1,0);(2)k=﹣2;(3)N的坐标为(![]() ,
, ![]() )、(
)、(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
【解析】
试题分析:(1)利用分解因式法解一元二次方程![]() 即可得出OA、OC的值,再根据点所在的位置即可得出A、C的坐标;
即可得出OA、OC的值,再根据点所在的位置即可得出A、C的坐标;
(2)根据点C的坐标利用待定系数法即可求出直线CD的解析式,根据点A、B的横坐标结合点E为线段AB的中点即可得出点E的横坐标,将其代入直线CD的解析式中即可求出点E的坐标,再利用待定系数法即可求出k值;
(3)假设存在,设点M的坐标为(m,﹣m+1),分别以BE为边、BE为对角线来考虑.根据菱形的性质找出关于m的方程,解方程即可得出点M的坐标,再结合点B、E的坐标即可得出点N的坐标.
试题解析:(1)∵![]() ,∴(x﹣1)(x﹣2)=0,∴
,∴(x﹣1)(x﹣2)=0,∴![]() =1,
=1,![]() =2,∵OA>OC,∴OA=2,OC=1,∴A(﹣2,0),C(1,0).
=2,∵OA>OC,∴OA=2,OC=1,∴A(﹣2,0),C(1,0).
(2)将C(1,0)代入y=﹣x+b中,得:0=﹣1+b,解得:b=1,∴直线CD的解析式为y=﹣x+1.
∵点E为线段AB的中点,A(﹣2,0),B的横坐标为0,∴点E的横坐标为﹣1.
∵点E为直线CD上一点,∴E(﹣1,2).
将点E(﹣1,2)代入![]() (k≠0)中,得:2=
(k≠0)中,得:2=![]() ,解得:k=﹣2.
,解得:k=﹣2.
(3)假设存在,设点M的坐标为(m,﹣m+1),以点B,E,M,N为顶点的四边形是菱形分两种情况(如图所示):
①以线段BE为边时,∵E(﹣1,2),A(﹣2,0),E为线段AB的中点,∴B(0,4),∴BE=![]() AB=
AB=![]() =
=![]() .
.
∵四边形BEMN为菱形,∴EM=![]() =BE=
=BE=![]() ,解得:m1=
,解得:m1=![]() ,m2=
,m2=![]() ,∴M(
,∴M(![]() ,
,![]() )或(
)或(![]() ,
,![]() ),∵B(0,4),E(﹣1,2),∴N(
),∵B(0,4),E(﹣1,2),∴N(![]() ,
, ![]() )或(
)或(![]() ,
,![]() );
);
②以线段BE为对角线时,MB=ME,∴![]() =
=![]() ,解得:m3=
,解得:m3=![]() ,∴M(
,∴M(![]() ,
,![]() ),∵B(0,4),E(﹣1,2),∴N(0﹣1+
),∵B(0,4),E(﹣1,2),∴N(0﹣1+![]() ,4+2﹣
,4+2﹣![]() ),即(
),即(![]() ,
,![]() ).
).
综上可得:坐标平面内存在点N,使以点B,E,M,N为顶点的四边形是菱形,点N的坐标为(![]() ,
, ![]() )、(
)、(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).

 天天向上口算本系列答案
天天向上口算本系列答案