题目内容
【题目】如图,△ACD和△BCE都是等腰直角三角形,∠ACD=∠BCE=90°,
(1)请判断线段AE和BD的数量关系和位置关系,并证明;
(2)若已知∠AED=135°,设∠AEC=α,当△BDE为等腰三角形时,求α的度数.

【答案】(1)AE=BD且AE⊥BD,理由见解析;(2)当△BDE为等腰三角形时,α的度数为112.5°、135°或90°.
【解析】试题分析:(1)根据![]() 和
和![]() 都是等腰直角三角形、
都是等腰直角三角形、![]() 即可得出
即可得出![]() 再由角的计算即可得出
再由角的计算即可得出![]() 利用全等三角形的判定定理SAS即可证出
利用全等三角形的判定定理SAS即可证出![]() 进而可得出
进而可得出![]() 延长AE,交CD于点H,交BD于点F,根据角的计算即可得出
延长AE,交CD于点H,交BD于点F,根据角的计算即可得出![]() 从而找出
从而找出![]()
(2)根据![]() 是等腰直角三角形即可得出
是等腰直角三角形即可得出![]() 结合
结合![]() 即可找出
即可找出![]() 由
由![]() 可得出
可得出![]() 进而得出
进而得出![]() 再根据三角形内角和定理即可得出
再根据三角形内角和定理即可得出![]() 分
分![]() 以及
以及![]() 三种情况考虑
三种情况考虑![]() 为等腰三角形,代入数据求出
为等腰三角形,代入数据求出![]() 值,此题得解.
值,此题得解.
试题解析:(1)AE=BD且AE⊥BD,理由如下:
∵△ACD和△BCE都是等腰直角三角形, ![]()
∴AC=DC,EC=BC.
![]()
∴∠ACE=∠DCB.
在△ACE和△DCB中, 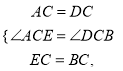
![]()
∴AE=DB,∠CAE=∠CDB.
延长AE,交CD于点H,交BD于点F,如图1所示。
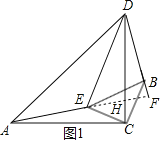
∵∠AHD=∠CHF=∠CDB+∠DFH,∠AHD=∠CAE+∠ACD,
![]()
∴AE⊥BD.
(2)∵△BCE是等腰直角三角形, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
在△DBE中, ![]()
△BDE为等腰三角形分三种情况:
①∠DEB=∠DBE,即![]()
![]()
②∠DEB=∠EDB,即![]()
![]()
③∠DBE=∠EDB,即![]()
![]()
综上所述:当△BDE为等腰三角形时, ![]() 的度数为112.5°、135°或90°.
的度数为112.5°、135°或90°.

练习册系列答案
相关题目