Question

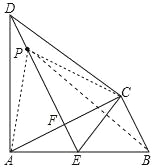
【题目】如图，△ABC中，∠ACB=90°，以AC为底边作等腰三角形△ACD，AD=CD，过点D作DE⊥AC，垂足为F，DE与AB相交于点E，连接CE．

（1）求证：AE=CE=BE；

（2）若AB=15cm，BC=9cm，点P是射线DE上的一点．则当点P为何处时，△PBC的周长最小，并求出此时△PBC的周长．

Answer 1

【答案】(1)、证明过程见解析；(2)、当P与E重合时，△PBC的周长最小值为24cm

【解析】

试题分析：(1)、首先证明EA=EC，再证明EC=EB即可解决问题．(2)、先说明P与E重合时△PBC的周长最小，最小值=AB+AC．

试题解析：(1)、∵DA=DC，DF⊥AC，∴AF=CF， ∴DE垂直平分线段AC，∴EA=EC， ∴∠EAC=∠ECA，

∵∠ACB=90°， ∴∠EAC+∠B=90°，∠ECA+∠ECB=90°， ∴∠ECB=∠B， ∴EC=EB=EA．

(2)、连接PB、PC、PA． 要使得△PBC的周长最小，只要PB+PC最小即可． ∵PB+PC=PA+PB≥AB，

∴当P与E重合时，PA+PB最小， ∴△PBC的周长最小值=AB+BC=15+9=24cm．