ЬтФПФкШн
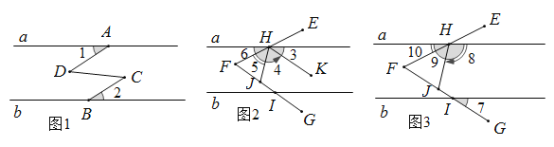
ЁОЬтФПЁПЮЪЬтБГОАЃКдкЁїABCжаЃЌABЁЂBCЁЂACШ§БпЕФГЄЗжБ№ЮЊ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЃЌЧѓетИіШ§НЧаЮЕФУцЛ§аЁЛдЭЌбЇдкНтД№етЕРЬтЪБЃЌЯШНЈСЂвЛИіе§ЗНаЮЭјИёЃЈУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЃЉЃЌдйдкЭјИёжаЛГіИёЕуЁїABCЃЈМДЁїABCШ§ИіЖЅЕуЖМдкаЁе§ЗНаЮЕФЖЅЕуДІЃЉЃЌШчЭМ1ЫљЪОетбљВЛашЧѓЁїABCЕФИпЃЌЖјНшгУЭјИёОЭФмМЦЫуГіЫќЕФУцЛ§ЃЎ
ЃЌЧѓетИіШ§НЧаЮЕФУцЛ§аЁЛдЭЌбЇдкНтД№етЕРЬтЪБЃЌЯШНЈСЂвЛИіе§ЗНаЮЭјИёЃЈУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЃЉЃЌдйдкЭјИёжаЛГіИёЕуЁїABCЃЈМДЁїABCШ§ИіЖЅЕуЖМдкаЁе§ЗНаЮЕФЖЅЕуДІЃЉЃЌШчЭМ1ЫљЪОетбљВЛашЧѓЁїABCЕФИпЃЌЖјНшгУЭјИёОЭФмМЦЫуГіЫќЕФУцЛ§ЃЎ

ЃЈ1ЃЉЧыФуНЋЁїABCЕФУцЛ§жБНгЬюаДдкКсЯпЩЯЃКЁЁЁЁЁЁЁЁ ЃЛ
ЃЈ2ЃЉЛЁїDEFЃЌDEЁЂEFЁЂDFШ§БпЕФГЄЗжБ№ЮЊ1ЁЂ3ЁЂ![]() ЃЌВЂХаЖЯШ§НЧаЮЕФаЮзДЃЌЫЕУїРэгЩЃЎ
ЃЌВЂХаЖЯШ§НЧаЮЕФаЮзДЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉЭММћЯъНтЃЛЁїDEFЪЧжБНЧШ§НЧаЮЃЎ
ЃЛЃЈ2ЃЉЭММћЯъНтЃЛЁїDEFЪЧжБНЧШ§НЧаЮЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉгУе§ЗНаЮЕФУцЛ§МѕШЅШ§ИіжБНЧШ§НЧаЮЕФУцЛ§МДПЩЃЛ
ЃЈ2ЃЉРћгУЙДЙЩЖЈРэЕФФцЖЈРэХаЖЈШ§НЧаЮЕФаЮзДЮЊжБНЧШ§НЧаЮ.
ЃЈ1ЃЉШчЯТЭМЫљЪОЃК
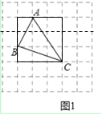
SЁїABC=3ЁС3Љ![]() ЁС1ЁС2Љ
ЁС1ЁС2Љ![]() ЁС2ЁС3Љ
ЁС2ЁС3Љ![]() ЁС1ЁС3=
ЁС1ЁС3=![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШчЭМ2ЫљЪОЃКЁїDEFМДЮЊЫљЧѓЃЛ
Ёп12+32=ЃЈ![]() ЃЉ2ЃЌ
ЃЉ2ЃЌ
ЁрЁїDEFЪЧжБНЧШ§НЧаЮЃЎ

ЁОЬтФПЁПФГаЃОйааЁАККзжЬ§аДЁББШШќЃЌУПЮЛбЇЩњЬ§аДККзж39Иі.БШШќНсЪјКѓЫцЛњГщВщВПЗжбЇЩњЬ§аДНсЙћЃЌЭМ1ЃЌЭМ2ЪЧИљОнГщВщНсЙћЛцжЦЕФЭГМЦЭМЕФвЛВПЗж.
зщБ№ | Ь§аДе§ШЗЕФИіЪ§x | ШЫЪ§ |
A | 0Ёмx<8 | 10 |
B | 8Ёмx<16 | 15 |
C | 16Ёмx<24 | 25 |
D | 24Ёмx<32 | m |
E | 32Ёмx<40 | n |

ИљОнвдЩЯаХЯЂНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉБОДЮЙВЫцЛњГщВщСЫЖрЩйУћбЇЩњЃЌЧѓГіmЃЌnЕФжЕВЂВЙШЋЭМ2ЕФЬѕаЮЭГМЦЭМЃЛ
ЃЈ2ЃЉЧѓГіЭМ1жаЁЯІСЕФЖШЪ§ЃЛ
ЃЈ3ЃЉИУаЃЙВга3000УћбЇЩњЃЌШчЙћЬ§аДе§ШЗЕФИіЪ§Щйгк24ИіЖЈЮЊВЛКЯИёЃЌЧыФуЙРМЦетЫљбЇаЃБОДЮБШШќЬ§аДВЛКЯИёЕФбЇЩњШЫЪ§.