题目内容
【题目】(1)如图甲是国际数学家大会会标,它是由四个相同的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积为13,每个直角三角形两直角边的和是5,求中间小正方形的面积为________ ;
(2)现有一张长为6.5cm,宽为2cm的纸片,如图乙,请你将它分割成6块,再拼合成一个正方形.(要求:先在图乙中画出分割线标明相应数据,再画出拼成的正方形的示意图,并标明相应数据)

【答案】(1)1;(2)见详解
【解析】
(1)可设直角三角形的两条直角边,根据勾股定理得到两条直角边的一个关系式,再结合已知条件联立解方程组,求出两条直角边的长.则小正方形的面积即为大正方形的面积减去4个直角三角形的面积;
(2)根据面积不变,可知要拼成的正方形的边长是![]() .13=4+9,故可以把它分割成4个直角边分别是2和3的直角三角形和两个长宽分别是1和0.5的矩形.
.13=4+9,故可以把它分割成4个直角边分别是2和3的直角三角形和两个长宽分别是1和0.5的矩形.
解:(1)设直角三角形的两条边分别为a、b(a>b),
则依题意有:![]()
①两边平方-②,得ab=6,
(a-b)2=(a+b)2-4ab=1,
∴a-b=1,
故小正方形的面积为1.
(2)如图所示: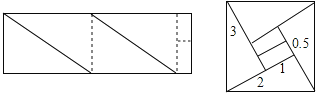

练习册系列答案
 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目




