Question

【题目】在△ABC中，AC=AB=5，一边上高为3，求底边BC的长（注意：请画出图形）．

Answer 1

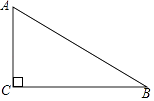
【答案】解：分三种情况：①当底边BC边上的高为3时，如图1所示，
∵在△ACD中，AB=AC=5，高AD=3，
∴BD=CD= =4，
∴BC=2BD=8；
②当腰上的高BD=3时，如图2所示：
则AD= =4，
∴CD=5﹣4=1，
∴BC= = = ；
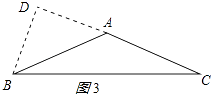
③当高在△ABC的外部时，如图3所示：
∵在△BCD中，AB=AC=5，高BD=3，
∴AD= =4，
∴CD=4+5=9，
∴BC= = =3 ；
综上所述：底边BC的长是8或 或3 ．



【解析】分三种情况：①当底边BC边上的高为3时；②当腰上的高BD=3时；③当高在△ABC的外部时；根据勾股定理先求得AD，根据线段的和差求得BD，根据勾股定理求得底边BC的长．
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识，掌握等腰三角形的两个底角相等（简称：等边对等角），以及对勾股定理的概念的理解，了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2．