题目内容
【题目】如图1，在平面直角坐标系中，直线AB与
轴交于点A，与
轴交于点B，与直线OC：
交于点C．
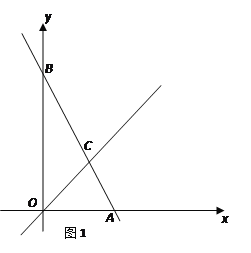
（1）若直线AB解析式为
，
①求点C的坐标；
②求△OAC的面积．
（2）如图2，作
的平分线ON，若AB⊥ON，垂足为E， OA＝4，P、Q分别为线段OA、OE上的动点，连结AQ与PQ，试探索AQ＋PQ是否存在最小值？若存在，求出这个最小值；若不存在，说明理由．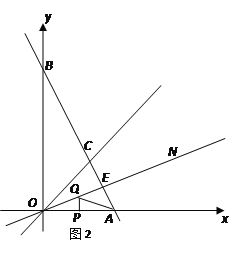
【答案】（1）①C（4，4）；②12；（2）存在，3
【解析】
试题（1）①联立两个函数式，求解即可得出交点坐标，即为点C的坐标；
②欲求△OAC的面积，结合图形，可知，只要得出点A和点C的坐标即可，点C的坐标已知，利用函数关系式即可求得点A的坐标，代入面积公式即可；
（2）在OC上取点M，使OM=OP，连接MQ，易证△POQ≌△MOQ，可推出AQ+PQ=AQ+MQ；若想使得AQ+PQ存在最小值，即使得A、Q、M三点共线，又AB⊥OP，可得∠AEO=∠CEO，即证△AEO≌△CEO（ASA），又OC=OA=4，利用△OAC的面积为6，即可得出AM=3，AQ+PQ存在最小值，最小值为3．
（1）①由题意，
解得
所以C（4，4）；
②把
代入
得，
，所以A点坐标为（6，0），
所以
；
（2）由题意，在OC上截取OM＝OP，连结MQ
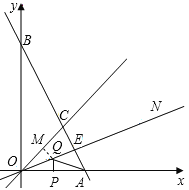
∵OQ平分∠AOC，
∴∠AOQ=∠COQ，
又OQ=OQ，
∴△POQ≌△MOQ（SAS），
∴PQ=MQ，
∴AQ+PQ=AQ+MQ，
当A、Q、M在同一直线上，且AM⊥OC时，AQ+MQ最小．
即AQ+PQ存在最小值．
∵AB⊥ON，所以∠AEO=∠CEO，
∴△AEO≌△CEO（ASA），
∴OC=OA=4，
∵△OAC的面积为12，所以AM=12÷4=3，
∴AQ+PQ存在最小值，最小值为3．
【题目】某园林专业户计划投资种植花卉及树木，根据市场调查与预测，种植树木的利润y1与投资量x成正比例关系，种植花卉的利润y2与投资量x的平方成正比例关系，并得到了表格中的数据．
投资量x（万元） | 2 |
种植树木利润y1（万元） | 4 |
种植花卉利润y2（万元） | 2 |
（1）分别求出利润y1与y2关于投资量x的函数关系式；
（2）如果这位专业户以8万元资金投入种植花卉和树木，设他投入种植花卉金额m万元，种植花卉和树木共获利利润W万元，直接写出W关于m的函数关系式，并求他至少获得多少利润？他能获取的最大利润是多少？
（3）若该专业户想获利不低于22万，在（2）的条件下，直接写出投资种植花卉的金额m的范围．
