题目内容
如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.(1)求直线AC的解析式;
(2)连接BM,如图2,动点P从点A出发,沿折线ABC方向以2个单位/秒的速度向终点C匀速运动,设△PMB的面积为S(S≠0),点P的运动时间为t秒,求S与t之间的函数关系式(要求写出自变量t的取值范围);
(3)在(2)的条件下,当t为何值时,∠MPB与∠BCO互为余角,并求此时直线OP与直线AC所夹锐角的正切值.

分析:(1)已知A点的坐标,就可以求出OA的长,根据OA=OC,就可以得到C点的坐标,根据待定系数法就可以求出函数解析式.
(2)点P的位置应分P在AB和BC上,两种情况进行讨论.当P在AB上时,△PMB的底边PB可以用时间t表示出来,高是MH的长,因而面积就可以表示出来.
(3)本题可以分两种情况进行讨论,当P点在AB边上运动时:设OP与AC相交于点Q连接OB交AC于点K,证明△AQP∽△CQO,根据相似三角形的对应边的比相等,以及勾股定理可以求出AQ,QC的长,在直角△OHB中,根据勾股定理,可以得到tan∠OQC.
当P点在BC边上运动时,可证△BHM∽△PBM和△PQC∽△OQA,根据相似三角形的对应边的比相等,就可以求出OK,KQ就可以求出.
(2)点P的位置应分P在AB和BC上,两种情况进行讨论.当P在AB上时,△PMB的底边PB可以用时间t表示出来,高是MH的长,因而面积就可以表示出来.
(3)本题可以分两种情况进行讨论,当P点在AB边上运动时:设OP与AC相交于点Q连接OB交AC于点K,证明△AQP∽△CQO,根据相似三角形的对应边的比相等,以及勾股定理可以求出AQ,QC的长,在直角△OHB中,根据勾股定理,可以得到tan∠OQC.
当P点在BC边上运动时,可证△BHM∽△PBM和△PQC∽△OQA,根据相似三角形的对应边的比相等,就可以求出OK,KQ就可以求出.
解答: 解:(1)过点A作AE⊥x轴垂足为E,如图(1)
解:(1)过点A作AE⊥x轴垂足为E,如图(1)
∵A(-3,4),
∴AE=4 OE=3,
∴OA=
=5,
∵四边形ABCO为菱形,
∴OC=CB=BA=0A=5,
∴C(5,0)(1分)
设直线AC的解析式为:y=kx+b,
∵
,
∴
,
∴直线AC的解析式为y=-
x+
.(1分)
(2)由(1)得M点坐标为(0,
),
∴OM=
,
如图(1),当P点在AB边上运动时
由题意得OH=4,
∴HM=OH-OM=4-
=
,
∴s=
BP•MH=
(5-2t)•
,
∴s=-
t+
(0≤t<
),2分
当P点在BC边上运动时,记为P1,
∵∠OCM=∠BCM,CO=CB,CM=CM,
∴△OMC≌△BMC,
∴OM=BM=
,∠MOC=∠MBC=90°,
∴S=
P1B•BM=
(2t-5)
,
∴S=
t-
(
<t≤5),2分
(3)设OP与AC相交于点Q连接OB交AC于点K,
∵∠AOC=∠ABC,
∴∠AOM=∠ABM,
∵∠MPB+∠BCO=90°,∠BAO=∠BCO,∠BAO+∠AOH=90°,
∴∠MPB=∠AOH,
∴∠MPB=∠MBH.
当P点在AB边上运动时,如图(2)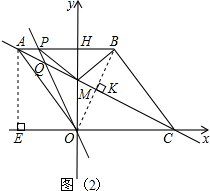
∵∠MPB=∠MBH,
∴PM=BM,
∵MH⊥PB,
∴PH=HB=2,
∴PA=AH-PH=1,
∴t=
,(1分)
∵AB∥OC,
∴∠PAQ=∠OCQ,
∵∠AQP=∠CQO,
∴△AQP∽△CQO,
∴
=
=
,
在Rt△AEC中,AC=
=
=4
,
∴AQ=
,QC=
,
在Rt△OHB中,OB=
=
=2
,
∵AC⊥OB,OK=KB,AK=CK,
∴OK=
,AK=KC=2
,
∴QK=AK-AQ=
,
∴tan∠OQC=
=
,(1分)
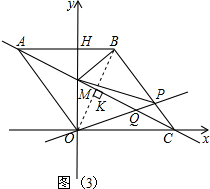
当P点在BC边上运动时,如图(3),
∵∠BHM=∠PBM=90°,∠MPB=∠MBH,
∴tan∠MPB=tan∠MBH,
∴
=
,即
=
,
∴BP=
,
∴t=
,(1分)
∴PC=BC-BP=5-
=
.
由PC∥OA,同理可证△PQC∽△OQA,
∴
=
,
∴
=
,
CQ=
AC=
,
∴QK=KC-CQ=
,
∵OK=
,
∴tan∠OQK=
=1.(1分)
综上所述,当t=
时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为
.
当t=
时,∠MPB与∠BCO互为余角,直线OP与直线AC所夹锐角的正切值为1.
 解:(1)过点A作AE⊥x轴垂足为E,如图(1)
解:(1)过点A作AE⊥x轴垂足为E,如图(1)∵A(-3,4),
∴AE=4 OE=3,
∴OA=
| AE2+OE2 |
∵四边形ABCO为菱形,
∴OC=CB=BA=0A=5,
∴C(5,0)(1分)
设直线AC的解析式为:y=kx+b,
∵
|
∴
|
∴直线AC的解析式为y=-
| 1 |
| 2 |
| 5 |
| 2 |
(2)由(1)得M点坐标为(0,
| 5 |
| 2 |
∴OM=
| 5 |
| 2 |
如图(1),当P点在AB边上运动时
由题意得OH=4,
∴HM=OH-OM=4-
| 5 |
| 2 |
| 3 |
| 2 |
∴s=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
∴s=-
| 3 |
| 2 |
| 15 |
| 4 |
| 5 |
| 2 |
当P点在BC边上运动时,记为P1,
∵∠OCM=∠BCM,CO=CB,CM=CM,
∴△OMC≌△BMC,
∴OM=BM=
| 5 |
| 2 |
∴S=
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∴S=
| 5 |
| 2 |
| 25 |
| 4 |
| 5 |
| 2 |
(3)设OP与AC相交于点Q连接OB交AC于点K,
∵∠AOC=∠ABC,
∴∠AOM=∠ABM,
∵∠MPB+∠BCO=90°,∠BAO=∠BCO,∠BAO+∠AOH=90°,
∴∠MPB=∠AOH,
∴∠MPB=∠MBH.
当P点在AB边上运动时,如图(2)

∵∠MPB=∠MBH,
∴PM=BM,
∵MH⊥PB,
∴PH=HB=2,
∴PA=AH-PH=1,
∴t=
| 1 |
| 2 |
∵AB∥OC,
∴∠PAQ=∠OCQ,
∵∠AQP=∠CQO,
∴△AQP∽△CQO,
∴
| AQ |
| CQ |
| AP |
| CO |
| 1 |
| 5 |
在Rt△AEC中,AC=
| AE2+EC2 |
| 42+82 |
| 5 |
∴AQ=
2
| ||
| 3 |
10
| ||
| 3 |
在Rt△OHB中,OB=
| HB2+HO2 |
| 22+42 |
| 5 |

∵AC⊥OB,OK=KB,AK=CK,
∴OK=
| 5 |
| 5 |
∴QK=AK-AQ=
4
| ||
| 3 |
∴tan∠OQC=
| OK |
| QK |
| 3 |
| 4 |
当P点在BC边上运动时,如图(3),
∵∠BHM=∠PBM=90°,∠MPB=∠MBH,
∴tan∠MPB=tan∠MBH,
∴
| BM |
| BP |
| HM |
| HB |
| ||
| BP |
| ||
| 2 |
∴BP=
| 10 |
| 3 |
∴t=
| 25 |
| 6 |
∴PC=BC-BP=5-
| 10 |
| 3 |
| 5 |
| 3 |
由PC∥OA,同理可证△PQC∽△OQA,
∴
| CQ |
| AQ |
| CP |
| AO |
∴
| CQ |
| AQ |
| 1 |
| 3 |
CQ=
| 1 |
| 4 |
| 5 |
∴QK=KC-CQ=
| 5 |
∵OK=
| 5 |
∴tan∠OQK=
| OK |
| KQ |
综上所述,当t=
| 1 |
| 2 |
| 3 |
| 4 |
当t=
| 25 |
| 6 |
点评:本题主要考查了利用待定系数法求函数的解析式,求三角函数值的问题可以转化为求直角三角形的边的比的问题.

练习册系列答案
相关题目
 23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′;
23、在数学上,为了确定平面上点的位置,我们常用下面的方法:如图甲,在平面内画两条互相垂直,并且有公共原点O的数轴,通常一条画成水平,叫x轴,另一条画成铅垂,叫y轴,这样,我们就说在平面上建立了一个平面直角坐标系,这是由法国数学家和哲学家笛卡尔创立的,这样我们就能确定平面上点的位置,例如,要确定点M的位置,只要作MP⊥x轴,MP⊥y轴,设垂足N,P在各自数轴上所表示的数分别为x,y,则x叫做点M的横坐标,y叫做点M的纵坐标,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),(1)△ABC在平面直角坐标系中的位置如图乙,请把△ABC向右平移3个单位,在平面直角坐标系中画出平移后的△A′B′C′; 在平面直角坐标系中,将一块腰长为
在平面直角坐标系中,将一块腰长为

 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点,点
点,点 再绕着点
再绕着点 点,这时点
点,这时点 与点
与点 为旋转中心时,点
为旋转中心时,点 点,点
点,点 点,点
点,点 点,小明发现P、
点,小明发现P、 两点关于点
两点关于点 中心对称.
中心对称.


 、
、 、
、 为旋转中心时,点
为旋转中心时,点 绕着点
绕着点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到
旋转180°得到 点;点
点;点 旋转180°得到点
旋转180°得到点 . 继续如此操作若干次得到点
. 继续如此操作若干次得到点 ,则点
,则点 的坐为.
的坐为. ,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),
,有序数对(x,y)叫做M点的坐标,如图甲,点M的坐标记作(2,3),