题目内容
如图,(1)已知:P为半径为5的⊙O内一点,过P点最短的弦长为8,则OP=
(2)在(1)的条件下,若⊙O内有一异于P点的Q点,过Q点的最短弦长为6,且这两条弦平行,求PQ的长.
(3)在(1)的条件下,过P点任作弦MN、AB,试比较PM•PN与PA•PB的大小关系,且写出比较过程.你
 能用一句话归纳你的发现吗?
能用一句话归纳你的发现吗?(4)在(1)的条件下,过P点的弦CD=
| 25 | 3 |
分析:(1过点P的最短的弦即为过点P垂直于OP的弦,根据垂径定理、勾股定理进行计算;
(2)根据(1)的方法求得OQ的长,进而求得PQ的长;
(3)根据相似三角形的判定及性质进行证明;
(4)过点P作直径EF,根据(3)中得到的结论,知PC•PD=PE•PF,再结合已知条件进行计算.
(2)根据(1)的方法求得OQ的长,进而求得PQ的长;
(3)根据相似三角形的判定及性质进行证明;
(4)过点P作直径EF,根据(3)中得到的结论,知PC•PD=PE•PF,再结合已知条件进行计算.
解答: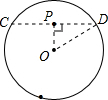 解:(1)连接OP,过点P作CD⊥OP于点P,连接OD.
解:(1)连接OP,过点P作CD⊥OP于点P,连接OD.
根据题意,得CD=8,OD=5.
根据垂径定理,得PD=4,
根据勾股定理,得OP=3;
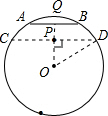
(2)根据平行线的性质和垂线的性质,知O、P、Q三点共线.
根据(1)的求解方法,得OQ=4,则PQ=1或7;
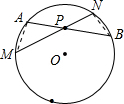 (3)连接AM、BN.
(3)连接AM、BN.
∵∠A=∠N,∠M=∠B,
∴△APM∽△NPB,
∴
=
,
即PM•PN=PA•PB;
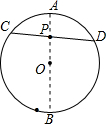
(4)作直径AB,根据相交弦定理,得PC•PD=PA•PB=(5-3)(5+3)=16,
又CD=
,
设PC=x,则PD=
-x,则有x(
-x)=16,
解,得x=3或x=
.
即PC=3或
,PD=
或3.
 解:(1)连接OP,过点P作CD⊥OP于点P,连接OD.
解:(1)连接OP,过点P作CD⊥OP于点P,连接OD.根据题意,得CD=8,OD=5.
根据垂径定理,得PD=4,
根据勾股定理,得OP=3;

(2)根据平行线的性质和垂线的性质,知O、P、Q三点共线.
根据(1)的求解方法,得OQ=4,则PQ=1或7;
 (3)连接AM、BN.
(3)连接AM、BN.∵∠A=∠N,∠M=∠B,
∴△APM∽△NPB,
∴
| PA |
| PM |
| PN |
| PB |
即PM•PN=PA•PB;

(4)作直径AB,根据相交弦定理,得PC•PD=PA•PB=(5-3)(5+3)=16,
又CD=
| 25 |
| 3 |
设PC=x,则PD=
| 25 |
| 3 |
| 25 |
| 3 |
解,得x=3或x=
| 16 |
| 3 |
即PC=3或
| 16 |
| 3 |
| 16 |
| 3 |
点评:此题的综合性较强,综合考查了相交弦定理、垂径定理、勾股定理以及相似三角形的判定及性质.

练习册系列答案
相关题目


 15、如图,?ABCD中,已知AB=9cm,AD=6cm,BE平分∠ABC交DC边于点E,则DE等于( )
15、如图,?ABCD中,已知AB=9cm,AD=6cm,BE平分∠ABC交DC边于点E,则DE等于( ) 如图,将一个长方形纸条折成如图的形状,若已知∠1=130°,则∠2=
如图,将一个长方形纸条折成如图的形状,若已知∠1=130°,则∠2= 如图.
如图.