题目内容
 如图.
如图.(1)已知AB∥CD,EF∥MN,且∠BOH=110°,求∠DHF和∠CGN的度数.
(2)请你观察(1)中的结果,找出其中的规律,并用文字表述出来.
(3)根据(2)中的结论,若两个角的两边分别平行,且其中一个角的度数是另一个角的2倍,求这两个角的度数.
分析:(1)根据平行线的性质由AB∥CD得到∠DHF=∠BOH=110°,再根据EF∥MN可得∠DHF+∠CGN=180°,即可计算出∠CGN的度数;
(2)观察两个角的两边的关系以及这两个角的大小关系;
(3)设一个角的度数为x,则另一个角的度数为2x,利用(2)中结论得到x+2x=180°,然后解方程即可.
(2)观察两个角的两边的关系以及这两个角的大小关系;
(3)设一个角的度数为x,则另一个角的度数为2x,利用(2)中结论得到x+2x=180°,然后解方程即可.
解答:解:(1)∵AB∥CD,
∴∠DHF=∠BOH=110°,
又∵EF∥MN,
∴∠DHF+∠CGN=180°,
∴∠CGN=180°-110°=70°;
(2)若两个角的两边分别平行,那么这两个角相等或互补;
(3)设一个角的度数为x,则另一个角的度数为2x,
∴x+2x=180°,
解得x=60°.
所以这两个角的度数分别为120°和60°.
∴∠DHF=∠BOH=110°,
又∵EF∥MN,
∴∠DHF+∠CGN=180°,
∴∠CGN=180°-110°=70°;
(2)若两个角的两边分别平行,那么这两个角相等或互补;
(3)设一个角的度数为x,则另一个角的度数为2x,
∴x+2x=180°,
解得x=60°.
所以这两个角的度数分别为120°和60°.
点评:本题考查了平行线的性质:两直线平行,同位角相等,同旁内角互补.也考查了若两个角的两边分别平行,那么这两个角相等或互补.

练习册系列答案
相关题目
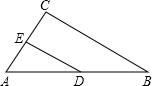 如图,△ABC中,已知AB=8,BC=6,CA=4,DE是中位线,则DE=( )
如图,△ABC中,已知AB=8,BC=6,CA=4,DE是中位线,则DE=( )| A、4 | B、3 | C、2 | D、1 |
 18、如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形:
18、如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形: 15、如图,?ABCD中,已知AB=9cm,AD=6cm,BE平分∠ABC交DC边于点E,则DE等于( )
15、如图,?ABCD中,已知AB=9cm,AD=6cm,BE平分∠ABC交DC边于点E,则DE等于( ) 2、如图,△ABC中,已知AB=AC=x,BC=6,则腰长x的取值范围是( )
2、如图,△ABC中,已知AB=AC=x,BC=6,则腰长x的取值范围是( )
