题目内容
【题目】如图,已知抛物线![]() 的顶点坐标为E(1,0),与
的顶点坐标为E(1,0),与![]() 轴的交点坐标为(0,1).
轴的交点坐标为(0,1).
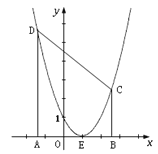

(1)求该抛物线的函数关系式.
(2)A、B是![]() 轴上两个动点,且A、B间的距离为AB=4,A在B的左边,过A作AD⊥
轴上两个动点,且A、B间的距离为AB=4,A在B的左边,过A作AD⊥![]() 轴交抛物线于D,
轴交抛物线于D,
过B作BC⊥![]() 轴交抛物线于C. 设A点的坐标为(
轴交抛物线于C. 设A点的坐标为(![]() ,0),四边形ABCD的面积为S.
,0),四边形ABCD的面积为S.
① 求S与![]() 之间的函数关系式.
之间的函数关系式.
② 求四边形ABCD的最小面积,此时四边形ABCD是什么四边形?
③ 当四边形ABCD面积最小时,在对角线BD上是否存在这样的点P,使得△PAE的周长最小,若存在,请求出点P的坐标及这时△PAE的周长;若不存在,说明理由.
【答案】(1)![]() (2)①
(2)①![]() ②四边形ABCD是正方形③2+
②四边形ABCD是正方形③2+![]()
【解析】试题分析:(1)先设抛物线的顶点式,然后把点(0,1)代入抛物线,可以求出抛物线的解析式.(2)①因为点A的坐标为(t,0),AB=4,所以点B的坐标为(t+4,0),分别把A,B两点的坐标代入抛物线得到C,D两点的坐标,得到线段AD和BC的长,可以用含t的式子表示直角梯形ABCD的面积.②根据①得到S关于t的二次函数,利用二次函数的性质,可以求出面积最小时t的值,并确定此时四边形的形状.③当四边形ABCD的面积最小时,ABCD是正方形,点A点C关于BD对称,根据两点之间线段最短,得到CE与BD的交点就是点P,然后求出△PAE的周长.
试题解析: (1)∵ 抛物线![]() 顶点为F(1,0)
顶点为F(1,0)
∴ ![]()
∵ 该抛线经过点E(0,1)
∴ ![]()
∴ ![]()
∴ ![]() ,
,
即所求抛物线的函数关系式为![]() .
.
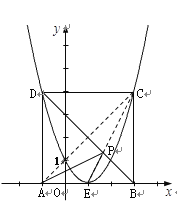
(2)① ∵ A点的坐标为(![]() ,0), AB=4,且点C、D在抛物线上,
,0), AB=4,且点C、D在抛物线上,
∴ B、C、D点的坐标分别为(![]() +4,0),(
+4,0),(![]() +4, (
+4, (![]() +3)2),(
+3)2),(![]() ,(
,(![]() -1)2).
-1)2).
∴ ![]()
② ![]() .
.
∴ 当![]() =-1时,四边形ABCD的最小面积为16,
=-1时,四边形ABCD的最小面积为16,
此时AD=BC=AB=DC=4,四边形ABCD是正方形.
③ 当四边形ABCD的面积最小时,四边形ABCD是正方形,其对角线BD上存在点P, 使得ΔPAE的周长最小.
∵AE=4(定值),
∴要使ΔPAE的周长最小,只需PA+PE最小.
∵此时四边形BCD是正方形,点A与点C关于BD所在直线对称,
∴由几何知识可知,P是直线CE与正方形ABCD对角线BD的交点.
∵点E、B、C、D的坐标分别为(1,0)(3,0)(3,4)(-1,4)
∴直线BD,EC的函数关系式分别为:y=-x+3, y=2x-2.
∴ P(![]() ,
,![]() )
)
在Rt△CEB中,CE=![]() ,
,
∴△PAE的最小周长=AE+AP+PE=AE+CP+PE=AE+CE=2+![]()

 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案【题目】森林公园的门票价格规定如下表:
购票人数 | 1~50人 | 51~100人 | 100人以上 |
每人门票价 | 13元 | 11元 | 9元 |
某校初一(5)(6)两个班共104人去游森林公园,其中(5)班人数较少,不到50人;(6)班人数较多,(6)班人数多于50人且少于100人.经估算,如果两班都是以班为单位分别购票则一共应付1240元;
(1)求这两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少元?