题目内容
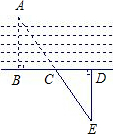
如图，要测量河两岸相对的两点A、B间的距离，先在过B点的AB的垂线L上取两点C、D，使CD=BC，再在过D点的垂线上取点E，使A、C、E在一条直线上，这时，△ACB≌△ECD，ED=AB，测ED的长就得AB得长，判定△ACB≌△ECD的理由是（ ）
| A．SAS | B．ASA | C．SSS | D．AAS |
∵AB⊥BC，DE⊥BC，
∴∠ABC=∠EDC=90°，
又CD=BC，
∠ACB=∠ECD，
∴△ABC≌△EDC
符合两角一边对应相等，所以利用的判定方法为ASA．
故选B．
∴∠ABC=∠EDC=90°，
又CD=BC，
∠ACB=∠ECD，
∴△ABC≌△EDC
符合两角一边对应相等，所以利用的判定方法为ASA．
故选B．
练习册系列答案
名师点睛字词句段篇系列答案
相关题目
13、如图，要测量河两岸相对的两点A、B间的距离，先从B处出发，与AB成90°角方向，向前走50米到C处立一根标杆，然后方向不变继续朝前走10米到D处，在D处沿垂直于BD的方向再走5米到达E处，使A（目标物），C（标杆）与E在同一直线上，则AB的长为
94、如图，要测量河两岸相对的两点A，B的距离，可以在AB的垂线BF上取两点C，D，使CD=BC，再定出BF的垂线DE，使A，C，E在一条直线上，这时测得的DE的长就是AB的长，为什么？
12、如图，要测量河两岸相对的两点A，B的距离，在AB的垂线BF上取两点C，D，使BC=CD，再定出BF的垂线DE，使A，C，E在一条直线上，这时测得DE=16米，则AB=
4、如图，要测量河两岸相对的两点A、B间的距离，先在过B点的AB的垂线L上取两点C、D，使CD=BC，再在过D点的垂线上取点E，使A、C、E在一条直线上，这时，△ACB≌△ECD，ED=AB，测ED的长就得AB得长，判定△ACB≌△ECD的理由是（ ）
如图，要测量河两岸相对的两点A，B的距离，在AB的垂线BF上取两点C，D，使