Question

【题目】已知抛物线的图象与轴交于和两点（点在点的左边），点为抛物线的顶点．

（1）求抛物线的函数解析式；

（2）画出此二次函数的大致图像；

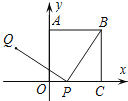
（3）点为线段上一点（点不与点、重合），过点作轴的垂线，与抛物线交于点，过点作交抛物线于点，过点作轴于点．若点在点左边，求当矩形的周长最大时点的横坐标．

Answer 1

【答案】（1）；（2）见解析；（3）－2

【解析】

（1）把A,B两点坐标分别代入解析式即可求解；

（2）求出对称轴，与坐标轴的交点可画出大致图像；

（3）设点M的横坐标为m，则PM和MN的长度可以用m表示，从而得出矩形的周长与m的函数关系式，最后利用二次函数的性质求解.

解：（1）把、两点坐标分别代入

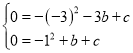
解得，，

∴

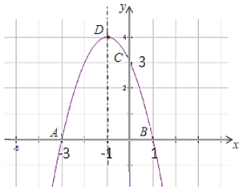
（2）函数与 轴的交点为 ；与 轴的交点坐标 ；顶点坐标 ;函数图像如图所示：

（3）由抛物线可知，对称轴为直线，

设点的横坐标为 ，则，，

∴矩形的周长，

∴当时矩形的周长最大．即的横坐标为-2.