题目内容
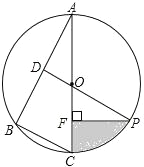
【题目】下面是小松设计的“做圆的内接等腰直角三角形”的尺规作图过程.
已知:⊙O.

求作:⊙O的内接等腰直角三角形.
作法:如图,
①作直径AB;

②分别以点A,B为圆心,以大于![]() 的同样长为半径作弧,两弧交于M,N两点;
的同样长为半径作弧,两弧交于M,N两点;
③作直线MN交⊙O于点C,D;
④连接AC,BC.
所以△ABC就是所求作的三角形.
根据小松设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明.
证明:∵AB是直径, C是⊙O上一点
∴ ∠ACB= ( ) (填写推理依据)
∵AC=BC( )(填写推理依据)
∴△ABC是等腰直角三角形.
【答案】(1)补全的图形如图所示见解析;(2)![]() 90°,直径所对的圆周角是直角, 线段垂直平分线上的点到线段两个端点的距离相等.
90°,直径所对的圆周角是直角, 线段垂直平分线上的点到线段两个端点的距离相等.
【解析】
(1)根据作法作出图形即可求解;
(2)根据直径的性质,线段的垂直平分线的性质即可解决问题;
(1)补全的图形如图所示:
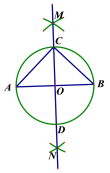
(2) 证明:∵AB是直径,C是⊙O上一点
∴∠ACB=90°(直径所对的圆周角是直角)(填写推理依据)
∵AC=BC (线段垂直平分线上的点到线段两个端点的距离相等)(填写推理依据)
∴△ABC是等腰直角三角形.
故答案为:90°,直径所对的圆周角是直角,线段垂直平分线上的点到线段两个端点的距离相等.

练习册系列答案
相关题目
【题目】某校食堂的中餐与晚餐的资费标准如下:
种类 | 单价 |
米饭 | 0.5元/份 |
A类套餐菜 | 3.5元/份 |
B类套餐菜 | 2.5元/份 |
小杰同学某星期从周一到周五每天的中餐与晚餐均在学校选用A类或B类中的一份套餐菜与一份米饭用餐,这五天共消费36元.请问小杰在这五天内,A,B类套餐菜各选用了多少次?