题目内容
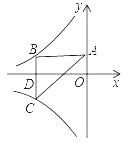
【题目】如图,在Rt△ABC中,∠ABC=90°,AB=BC,点E为线段AB上一动点(不与点A,B重合),连接CE,将∠ACE的两边CE,CA分别绕点C顺时针旋转90°,得到射线CE,,CA,,过点A作AB的垂线AD,分别交射线CE,,CA,于点F,G.
(1)依题意补全图形;
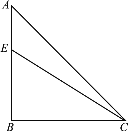
(2)若∠ACE=α,求∠AFC 的大小(用含α的式子表示);
(3)用等式表示线段AE,AF与BC之间的数量关系,并证明.
【答案】(1)补全的图形如图所示见解析;(2)∠AFC =α+45°;(3)AE,AF与BC之间的数量关系为![]() .证明见解析.
.证明见解析.
【解析】
(1)利用旋转的性质进而得出对应点位置进而得出答案;(2)根据旋转得出∠ECF=∠ACG=90°,∠FCG=∠ACE=α,最后用三角形的外角的性质即可得出结论;(3)借助(2)的结论判断出△ACE≌△GCF(ASA),得出AE=FG,再用勾股定理得出AG=![]()
AC,AC=![]() BC,即可得出结论.
BC,即可得出结论.
(1)补全的图形如图所示.
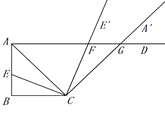
(2)解:由题意可知,∠ECF=∠ACG=90°
∴∠FCG=∠ACE=α
∵过点A作AB的垂线AD
∴∠BAD=90°
∵AB=BC,∠ABC=90°,
∴∠ACB=∠CAD= 45°
∵∠ACG=90°
∴∠AGC=45°
∴∠AFC =α+45°
(3)AE,AF与BC之间的数量关系为![]()
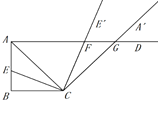
证明:由(2)可知∠DAC=∠AGC=45°
∴CA=CG
∵∠ACE =∠GCF,∠CAE =∠CGF
∴△ACE ≌△GCF
∴AE =FG.
在Rt△ACG中,
∴![]()
∴![]()
∵![]()
∴![]()

【题目】为了了解江城中学学生的身高情况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成如图所示的统计图表.
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
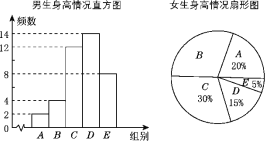
根据图表中提供的信息,回答下列问题:
(1)在样本中,男生身高的中位数落在________组(填组别序号),女生身高在B组的人数有________人;
(2)在样本中,身高在150≤x<155之间的人数共有________人,身高人数最多的在________组(填组别序号);
(3)已知该校共有男生500人、女生480人,请估计身高在155≤x<165之间的学生有多少人
【题目】二次函数![]() (a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
(a、b、c为常数且a≠0)中的x与y的部分对应值如下表:
x | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | 5 |
y | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | 12 |
给出了结论:
(1)二次函数![]() 有最小值,最小值为﹣3;
有最小值,最小值为﹣3;
(2)当![]() 时,y<0;
时,y<0;
(3)二次函数![]() 的图象与x轴有两个交点,且它们分别在y轴两侧.
的图象与x轴有两个交点,且它们分别在y轴两侧.
则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0