题目内容
【题目】如图1,已知平行四边形ABCD顶点A的坐标为(2,6),点B在y轴上,且AD∥BC∥x轴,过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),点F(m,6)是线段AD上一动点,直线OF交BC于点E.
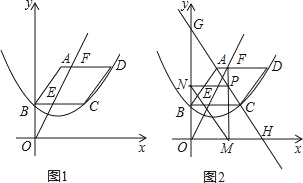
(1)求抛物线的表达式;
(2)设四边形ABEF的面积为S,请求出S与m的函数关系式,并写出自变量m的取值范围;
(3)如图2,过点F作FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,垂足为N,连接MN,直线AC分别交x轴,y轴于点H,G,试求线段MN的最小值,并直接写出此时m的值.
【答案】(1)抛物线解析式为y=![]() x2﹣x+3;(2)S=
x2﹣x+3;(2)S=![]() m﹣3(2<m≤6);(3)当m=
m﹣3(2<m≤6);(3)当m=![]() 时,MN最小=
时,MN最小=![]() .
.
【解析】试题分析:(1)根据平行四边形的性质和抛物线的特点确定出点D,然而用待定系数法确定出抛物线的解析式.(2)根据AD∥BC∥x轴,且AD,BC间的距离为3,BC,x轴的距离也为3,F(m,6),确定出E(![]() ,3),从而求出梯形的面积.(3)先求出直线AC解析式,然后根据FM⊥x轴,表示出点P(m,﹣
,3),从而求出梯形的面积.(3)先求出直线AC解析式,然后根据FM⊥x轴,表示出点P(m,﹣![]() m+9),最后根据勾股定理求出MN=
m+9),最后根据勾股定理求出MN=![]() ,从而确定出MN最大值和m的值.
,从而确定出MN最大值和m的值.
试题解析:(1)∵过B,C,D三点的抛物线y=ax2+bx+c(a≠0)的顶点坐标为(2,2),
∴点C的横坐标为4,BC=4,
∵四边形ABCD为平行四边形,
∴AD=BC=4,
∵A(2,6),
∴D(6,6),
设抛物线解析式为y=a(x﹣2)2+2,
∵点D在此抛物线上,
∴6=a(6﹣2)2+2,
∴a=![]() ,
,
∴抛物线解析式为y=![]() (x﹣2)2+2=
(x﹣2)2+2=![]() x2﹣x+3,
x2﹣x+3,
(2)∵AD∥BC∥x轴,且AD,BC间的距离为3,BC,x轴的距离也为3,F(m,6)
∴E(![]() ,3),
,3),
∴BE=![]() ,
,
∴S=![]() (AF+BE)×3=
(AF+BE)×3=![]() (m﹣2+
(m﹣2+![]() )×3=
)×3=![]() m﹣3
m﹣3
∵点F(m,6)是线段AD上,
∴2≤m≤6,
即:S=![]() m﹣3(2≤m≤6).
m﹣3(2≤m≤6).
(3)∵抛物线解析式为y=![]() x2﹣x+3,
x2﹣x+3,
∴B(0,3),C(4,3),
∵A(2,6),
∴直线AC解析式为y=﹣![]() x+9,
x+9,
∵FM⊥x轴,垂足为M,交直线AC于P
∴P(m,﹣![]() m+9),(2≤m≤6)
m+9),(2≤m≤6)
∴PN=m,PM=﹣![]() m+9,
m+9,
∵FM⊥x轴,垂足为M,交直线AC于P,过点P作PN⊥y轴,
∴∠MPN=90°,
∴MN=![]() =
=![]() =
=![]()
∵2≤m≤6,
∴当m=![]() 时,MN最小=
时,MN最小=![]() =
=![]() .
.

 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案【题目】某校为了选拔学生参加“汉字听写大赛”,对九年级一班、二班各10名学生进行汉字听写测试.计分采用10分制(得分均取整数),成绩达到6分或6分以上为及格,得到9分为优秀,成绩如表1所示,并制作了成绩分析表(表2).
表1
一班 | 5 | 8 | 8 | 9 | 8 | 10 | 10 | 8 | 5 | 5 |
二班 | 10 | 6 | 6 | 9 | 10 | 4 | 5 | 7 | 10 | 8 |
表2
班级 | 平均数 | 中位数 | 众数 | 方差 | 及格率 | 优秀率 |
一班 | 7.6 | 8 | 3.82 | 70% | 30% | |
二班 | b | 7.5 | 10 | 4.94 | 80% | 40% |
(1)在表2中,a= ,b= ;
(2)有人说二班的及格率、优秀率均高于一班,所以二班比一班好;但也有人认为一班成绩比二班好,请你给出坚持一班成绩好的两条理由;
(3)一班、二班获满分的中同学性别分别是1男1女、2男1女,现从这两班获满分的同学中各抽1名同学参加“汉字听写大赛”,用树状图或列表法求出恰好抽到1男1女两位同学的概率.
【题目】我市举行“第十七届中小学生书法大赛”作品比赛,已知每幅参赛作品成绩记为![]() ,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
,组委会从1000幅书法作品中随机抽取了部分参赛作品,统计了它们的成绩,并绘制成如下统计图表.
分数段 | 频数 | 百分比 |
| 38 | 0.38 |
| ________ | 0.32 |
| ________ | ________ |
| 10 | 0.1 |
合计 | ________ | 1 |

根据上述信息,解答下列问题:
(1)这次书法作品比赛成绩的调查是采用_____(填“普查”或“抽样调查”),样本是_____.
(2)完成上表,并补全书法作品比赛成绩频数直方图.
(3)若80分(含80分)以上的书法作品将被评为等级奖,试估计全市获得等级奖的数量.