题目内容
一次函数y=-３x-４与x轴交于（ ），与y轴交于（ ），y随x的增大而___________.
，
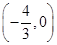，减少根据一次函数图象上点的坐标特征，与x轴相交时：y=0，与y轴相交时，x=0，可以求出交点坐标，再根据一次函数的性质：k＞0，y随x的增大而增大，函数从左到右上升；k＜0，y随x的增大而减小，函数从左到右下降可得答案．
解：一次函数y=-3x-4与x轴相交时：y=0，∴-3x-4=0，
x=-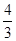
，
∴与x轴的交点为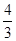：（-，0）；
与y轴相交时，x=0，
∴y=-4，
∴与y轴的交点为：（0，-4）；
∵一次函数y=-3x-4中，
-3＜0，
∴y随x的增大而减小，
故答案为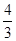：（-，0）；（0，-4）；减小．
解：一次函数y=-3x-4与x轴相交时：y=0，∴-3x-4=0，
x=-
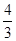，∴与x轴的交点为：（-
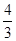，0）；与y轴相交时，x=0，
∴y=-4，
∴与y轴的交点为：（0，-4）；
∵一次函数y=-3x-4中，
-3＜0，
∴y随x的增大而减小，
故答案为：（-
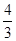，0）；（0，-4）；减小．
练习册系列答案
相关题目
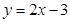的图像与x轴交点坐标为________,与y轴的交点坐标为____________。
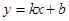经过点（1，2）和点（
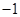，4），求这条直线的解析式.
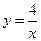的图像交于 A（2，2），B(－1，m)，求一次函数的解析式．
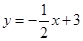向下平移___________个单位，就可以得到直线
．
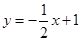