题目内容
【题目】如图,AD是![]() 的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).
的中线,E是AD上一点,连接BE并延长交AC于点F,若EF=AF, BE=7.5, CF=6,则EF=( ).
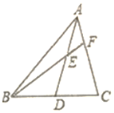
A.2.5B.2C.1.5D.1
【答案】C
【解析】
延长AD,使DG=AD,连接BG,由“SAS”可证△ADC≌△GDB,可得AC=DG=CF+AF=6+AF,∠DAC=∠G,由等腰三角形的性质可得BE=BG=7.5,即可求EF的长.
解:如图,延长AD,使DG=AD,连接BG,
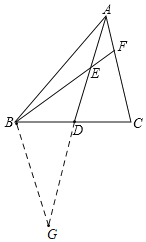
∵AD是△ABC的中线,
∴BD=CD,且DG=AD,∠ADC=∠BDG,
∴△ADC≌△GDB(SAS),
∴AC=DG=CF+AF=6+AF,∠DAC=∠G,
∵EF=AF,
∴∠DAC=∠AEF,
∴∠G=∠AEF=∠BEG,
∴BE=BG=7.5,
∴6+AF=BG=7.5,
∴AF=1.5=EF,
故选择:C.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
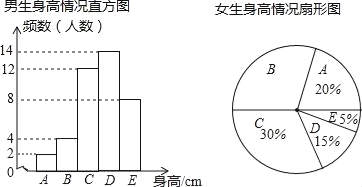
【题目】为了了解某校学生的身高状况,随机对该校男生、女生的身高进行抽样调查.已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制如图所示的统计图表:
组别 | 身高(cm) |
A | x<150 |
B | 150≤x<155 |
C | 155≤x<160 |
D | 160≤x<165 |
E | x≥165 |
已知女生身高在A组的有8人,根据图表中提供的信息,回答下列问题:
(1)男生身高的中位数落在 组(填组别字母序号);
(2)在样本中,身高在150≤x<155之间的人数共有 人,身高人数最多的在 组(填组别序号);
(3)已知该校共有男生400人、女生420人,请估计身高不足160cm的学生约有多少人?