题目内容
【题目】阅读下面材料:
小天在学习锐角三角函数中遇到这样一个问题:在Rt△ABC中,∠C=90°,∠B=22.5°,则tan22.5°=
小天根据学习几何的经验,先画出了几何图形(如图1),他发现22.5°不是特殊角,但它是特殊角45°的一半,若构造有特殊角的直角三角形,则可能解决这个问题.于是小天尝试着在CB边上截取CD=CA,连接AD(如图2),通过构造有特殊角(45°)的直角三角形,经过推理和计算使问题得到解决.
请回答:tan22.5°= .
参考小天思考问题的方法,解决问题:
如图3,在等腰△ABC 中,AB=AC,∠A=30°,请借助△ABC,构造出15°的角,并求出该角的正切值.
【答案】![]() ﹣1;解: 如图3,延长BA到D,使AD=AB,则AB=AD=AC,
﹣1;解: 如图3,延长BA到D,使AD=AB,则AB=AD=AC,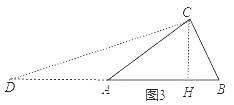 ∴∠D=∠ACD,∵∠CAB=∠D+∠ACD=30°, ∴∠D=15°,作CH⊥AB于H,设CH=x,则AC=2x,AH=
∴∠D=∠ACD,∵∠CAB=∠D+∠ACD=30°, ∴∠D=15°,作CH⊥AB于H,设CH=x,则AC=2x,AH= ![]() x,∴AD=AC=2x,∴DH=AD+AH=(2+
x,∴AD=AC=2x,∴DH=AD+AH=(2+ ![]() )x,在Rt△DCH中,tanD=
)x,在Rt△DCH中,tanD= ![]() ,即tan15°=2﹣
,即tan15°=2﹣ ![]()
【解析】如图2,设CD=CA=a,则AD= ![]() a,
a,
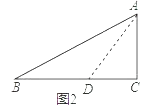
∵∠B=22.5°,∠ADC=45°,
∴∠DAB=22.5°,
∴∠DAB=∠B,
∴DB=DA= ![]() a,
a,
∴BC=BD+CD=( ![]() +1)a,
+1)a,
在Rt△ABC中,tanB= ![]() ,
,
即tan22.5°= ![]() ﹣1;
﹣1;
【考点精析】认真审题,首先需要了解三角形的外角(三角形一边与另一边的延长线组成的角,叫三角形的外角;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角),还要掌握锐角三角函数的定义(锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数)的相关知识才是答题的关键.

【题目】列方程组解应用题:
为了保护环境,深圳某公交公司决定购买一批共10台全新的混合动力公交车,现有A、B两种型号,其中每台的价格,年省油量如下表:
A | B | |
价格(万元/台) | a | b |
节省的油量(万升/年) | 2.4 | 2 |
经调查,购买一台A型车比购买一台B型车多20万元,购买2台A型车比购买3台B型车少60万元.
(1)请求出a和b;
(2)若购买这批混合动力公交车每年能节省22.4万汽油,求购买这批混合动力公交车需要多少万元?



