题目内容
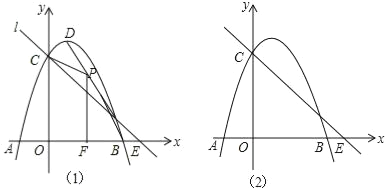
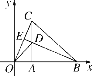
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,
,![]() .点
.点![]() 为
为![]() 轴上一动点,过点
轴上一动点,过点![]() 且垂直于
且垂直于![]() 轴的直线分别交直线
轴的直线分别交直线![]() 及抛物线于点
及抛物线于点![]() ,
,![]() .
.
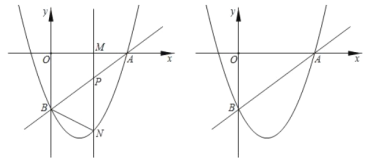
(1)填空:点![]() 的坐标为_________,抛物线的解析式为_________;
的坐标为_________,抛物线的解析式为_________;
(2)当点![]() 在线段
在线段![]() 上运动时(不与点
上运动时(不与点![]() ,
,![]() 重合),
重合),
①当![]() 为何值时,线段
为何值时,线段![]() 最大值,并求出
最大值,并求出![]() 的最大值;
的最大值;
②求出使![]() 为直角三角形时
为直角三角形时![]() 的值;
的值;
(3)若抛物线上有且只有三个点![]() 到直线
到直线![]() 的距离是
的距离是![]() ,请直接写出此时由点
,请直接写出此时由点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形的面积.
构成的四边形的面积.
【答案】(1)![]() ,
,![]() ;
;
(2)①当![]() 时,
时,![]() 有最大值是3; ②使
有最大值是3; ②使![]() 为直角三角形时
为直角三角形时![]() 的值为3或
的值为3或![]() ;
;
(3)点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形的面积为:6或
构成的四边形的面积为:6或![]() 或
或![]() .
.
【解析】
(1)把点A坐标代入直线表达式y=![]() ,求出a=3,把点A、B的坐标代入二次函数表达式,即可求解;
,求出a=3,把点A、B的坐标代入二次函数表达式,即可求解;
(2)①设:点P(m,![]() ),N(m,
),N(m,![]() )求出PN值的表达式,即可求解;②分∠BNP=90°、∠NBP=90°、∠BPN=90°三种情况,求解即可;
)求出PN值的表达式,即可求解;②分∠BNP=90°、∠NBP=90°、∠BPN=90°三种情况,求解即可;
(3)若抛物线上有且只有三个点N到直线AB的距离是h,则只能出现:在AB直线下方抛物线与过点N的直线与抛物线有一个交点N,在直线AB上方的交点有两个,分别求解即可.
解:(1)把点![]() 坐标代入直线表达式
坐标代入直线表达式![]() ,
,
解得:![]() ,则:直线表达式为:
,则:直线表达式为:![]() ,令
,令![]() ,则:
,则:![]() ,
,
则点![]() 坐标为
坐标为![]() ,
,
将点的坐标代入二次函数表达式得:
![]() ,
,
把点![]() 的坐标代入二次函数表达式得:
的坐标代入二次函数表达式得:![]() ,
,
解得:![]() ,
,
故:抛物线的解析式为:![]() ,
,
故:答案为:![]() ,
,![]() ;
;
(2)①∵![]() 在线段
在线段![]() 上,且
上,且![]() 轴,
轴,
∴点![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴抛物线开口向下,
∴当![]() 时,
时,![]() 有最大值是3,
有最大值是3,
②当![]() 时,点
时,点![]() 的纵坐标为-3,
的纵坐标为-3,
把![]() 代入抛物线的表达式得:
代入抛物线的表达式得:![]() ,解得:
,解得:![]() 或0(舍去
或0(舍去![]() ),
),
∴![]() ;
;
当![]() 时,∵
时,∵![]() ,两直线垂直,其
,两直线垂直,其![]() 值相乘为-1,
值相乘为-1,
设:直线![]() 的表达式为:
的表达式为:![]() ,
,
把点![]() 的坐标代入上式,解得:
的坐标代入上式,解得:![]() ,则:直线
,则:直线![]() 的表达式为:
的表达式为:![]() ,
,
将上式与抛物线的表达式联立并解得:![]() 或0(舍去
或0(舍去![]() ),
),
当![]() 时,不合题意舍去,
时,不合题意舍去,
故:使![]() 为直角三角形时
为直角三角形时![]() 的值为3或
的值为3或![]() ;
;
(3)∵![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,则:
,则:![]() ,
,![]() ,
,
∵![]() 轴,
轴,
∴![]() ,
,
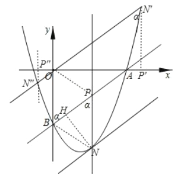
若抛物线上有且只有三个点![]() 到直线
到直线![]() 的距离是
的距离是![]() ,
,
则只能出现:在![]() 直线下方抛物线与过点
直线下方抛物线与过点![]() 的直线与抛物线有一个交点
的直线与抛物线有一个交点![]() ,在直线
,在直线![]() 上方的交点有两个.
上方的交点有两个.
当过点![]() 的直线与抛物线有一个交点
的直线与抛物线有一个交点![]() ,
,
点![]() 的坐标为
的坐标为![]() ,设:点
,设:点![]() 坐标为:
坐标为:![]() ,
,
则:![]() ,过点
,过点![]() 作
作![]() 的平行线,
的平行线,
则点![]() 所在的直线表达式为:
所在的直线表达式为:![]() ,将点
,将点![]() 坐标代入,
坐标代入,
解得:过![]() 点直线表达式为:
点直线表达式为:![]() ,
,
将拋物线的表达式与上式联立并整理得:![]() ,
,
![]() ,
,
将![]() 代入上式并整理得:
代入上式并整理得:![]() ,
,
解得:![]() ,则点
,则点![]() 的坐标为
的坐标为![]() ,
,
则:点![]() 坐标为
坐标为![]() ,则:
,则:![]() ,
,
∵![]() ,
,![]() ,∴四边形
,∴四边形![]() 为平行四边形,则点
为平行四边形,则点![]() 到直线
到直线![]() 的距离等于点
的距离等于点![]() 到直线
到直线![]() 的距离,
的距离,
即:过点![]() 与
与![]() 平行的直线与抛物线的交点为另外两个
平行的直线与抛物线的交点为另外两个![]() 点,即:
点,即:![]() 、
、![]() ,
,
直线![]() 的表达式为:
的表达式为:![]() ,将该表达式与二次函数表达式联立并整理得:
,将该表达式与二次函数表达式联立并整理得:
![]() ,解得:
,解得:![]() ,
,
则点![]() 、
、![]() 的横坐标分别为
的横坐标分别为![]() ,
,![]() ,
,
作![]() 交直线
交直线![]() 于点
于点![]() ,
,
则![]() ,
,
作![]() 轴,交
轴,交![]() 轴于点
轴于点![]() ,则:
,则:![]() ,
,![]() ,
,
![]() ,
,
则:![]() ,
,
同理:![]() ,
,
故:点![]() ,
,![]() ,
,![]() ,
,![]() 构成的四边形的面积为:6或
构成的四边形的面积为:6或![]() 或
或![]() .
.

【题目】在一个不透明的口袋里装有颜色不同的黑、白两种颜色的球共4个,某学习小组进行摸球试验,将球搅匀后从中随机摸出一个球记下颜色,再放回,下表是活动进行中的一组统计数据:
摸球的次数n | 100 | 150 | 200 | 500 | 800 | 1000 |
摸到黑球的次数m | 23 | 33 | 60 | 130 | 202 | 251 |
摸到黑球的频率 |
|
|
|
|
|
|
![]() 当n很大时,估计从袋中摸出一个黑球的概率是______;
当n很大时,估计从袋中摸出一个黑球的概率是______;
![]() 试估算口袋中白球有______个;
试估算口袋中白球有______个;
![]() 在
在![]() 的条件下,若从中先换出一球,不放回,摇匀后再摸出一球,请用列表或树状图的方法求两次都摸到白球的概率.
的条件下,若从中先换出一球,不放回,摇匀后再摸出一球,请用列表或树状图的方法求两次都摸到白球的概率.