题目内容
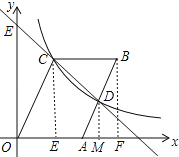
【题目】如图,OABC的顶点A的坐标为(3,0),∠COA=60°,D为边AB的中点,反比例函数y=![]() (k>0)的图象经过C、D两点,直线CD交y轴于点E,则OE的长为 .
(k>0)的图象经过C、D两点,直线CD交y轴于点E,则OE的长为 .

【答案】3![]()
【解析】
试题分析:作CE⊥x轴于点E,过B作BF⊥x轴于F,过D作DM⊥x轴于M,设C的坐标为(x,![]() x),表示出D的坐标,将C、D两点坐标代入反比例函数的解析式,解关于x的方程求出x即可得到点C、D的坐标,进而求得直线CD的解析式,最后计算该直线与y轴交点坐标即可得出结果.
x),表示出D的坐标,将C、D两点坐标代入反比例函数的解析式,解关于x的方程求出x即可得到点C、D的坐标,进而求得直线CD的解析式,最后计算该直线与y轴交点坐标即可得出结果.
解:作CE⊥x轴于点E,则∠CEO=90°,
过B作BF⊥x轴于F,过D作DM⊥x轴于M,则BF=CE,DM∥BF,BF=CE,
∵D为AB的中点,
∴AM=FM,
∴DM=![]() BF,
BF,
∵∠COA=60°,
∴∠OCE=30°,
∴OC=2OE,CE=![]() OE,
OE,
∴设C的坐标为(x,![]() x),
x),
∴AF=OE=x,CE=BF=![]() x,OE=AF=x,DM=
x,OE=AF=x,DM=![]() x,
x,
∵四边形OABC是平行四边形,A(3,0),
∴OF=3+x,OM=3+![]() x,
x,
即D点的坐标为(3+![]() x,
x,![]() x),
x),
把C、D的坐标代入y=![]() 得:k=x
得:k=x![]() x=(3+
x=(3+![]() x)
x)![]() x,
x,
解得:x1=2,x2=0(舍去),
∴C(2,2![]() ),D(4,
),D(4,![]() ),
),
设直线CD解析式为:y=ax+b,则
![]() ,
,
解得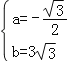 ,
,
∴直线CD解析式为y=﹣![]() x+3
x+3![]() ,
,
∴当x=0时,y=3![]() ,
,
∴E(0,3![]() ),即OE=3
),即OE=3![]() .
.
故答案为:3![]()

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目