Question

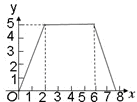
如图，梯形ABCD中，AB∥DC，DE⊥AB，CF⊥AB，且AE=EF=FB=5，DE=12,动点P从点A出发，沿折线AD-DC-CB以每秒1个单位长的速度运动到点B停止.设运动时间为t秒，y=S_△EPF，则y与t的函数图象大致是(     )

Answer 1

A.

试题分析：分三段考虑，①点P在AD上运动，②点P在DC上运动，③点P在BC上运动，分别求出y与t的函数表达式，继而可得出函数图象．
如图：

在Rt△ADE中，AD==13，
在Rt△CFB中，BC=，
①点P在AD上运动：
过点P作PM⊥AB于点M，则PM=APsin∠A=，
此时y=EF×PM=t，为一次函数；
②点P在DC上运动，y=EF×DE=30；
③点P在BC上运动，过点P作PN⊥AB于点N，则PN=BPsin∠B=（AD+CD+BC-t）=，
则y=EF×PN=，为一次函数．
综上可得选项A的图象符合．
故选A．
考点: 动点问题的函数图象．