Question

【题目】背景知识：

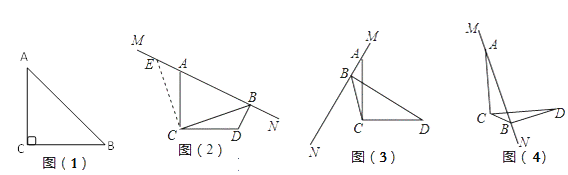
如图（2），在Rt△ABC中，∠ACB=90°，，则：.

（1）解决问题：

如图（2），∠ACD = 90°，AC = DC,MN是过点A的直线，过点D作DB⊥MN于点B，连接CB，试探究线段BA、BC、BD之间的数量关系.

不妨过点C作CE⊥CB,与MN交于点E，易发现图中出现了一对全等三角形，即 ≌ ，由此可得线段BA、BC、BD之间的数量关系是: .

（2）类比探究：

将图（2）中的MN绕点A旋转到图（3）的位置，其它条件不变，试探究线段BA、BC、BD之间的数量关系，并证明.

（3）拓展应用：

将图（2）中的MN绕点A旋转到图（4）的位置，其它条件不变，若BD=2，BC=，则AB的长为 .

Answer 1

【答案】（1）；(2) BD—AB=BC，理由详见解析；（3）4.

【解析】

（1）利用ASA证得，所以AE=BD，EB=AE+AB=BD+AB∵∴

（2）过点C作CE⊥CB, 与MN交于点E，利用ASA证得△ACE≌△DCB，进而求得线段之间的关系，同（1），即可证出.

（3）过点C作EC⊥CB交MN于点E，同（2），可证：，即可求出AB的长.

（1）

(2) BD—AB=BC .

过点C作CE⊥CB, 与MN交于点E,则∠ECB=90°

∴∠ECB+∠BCA=∠ACD+∠BCA,即：∠ECA=∠BCD.

∵DB⊥MN, ∴∠ABD=∠ACD=90°,

记AC与BD的交点为点F，则∠BFA=∠DFC， ∴∠BAF=∠FDC

在△ACE与△DCB中，

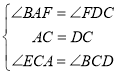
∴△ACE≌△DCB（ASA）

∴AE=BD, CE=CB

∴在Rt△BCE中, BE=BC，

∴BD =AE=BA+BE= BA+BC

即BD—AB=BC .

(3)

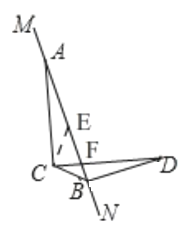
如图所示，过点C作EC⊥CB交MN于点E

同（2），可证：

∴AE=BD=2