题目内容
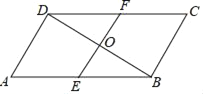
【题目】如图,E、F为菱形ABCD对角线上的两点,∠ADE=∠CDF,要判定四边形BFDE是正方形,需添加的条件是( )
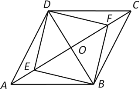
A.AE=CFB.OE=OFC.∠EBD=45°D.∠DEF=∠BEF
【答案】C
【解析】
从对角线的角度看,一个四边形需满足其两条对角线垂直、平分且相等才能判定是正方形,由于菱形的对角线已经垂直,所以要判定四边形BFDE是正方形,只需证明BD和EF相等且平分,据此逐项判断即可.
解:∵四边形ABCD是菱形,∴AO=CO,BO=DO,AC⊥BD,
A、若AE=CF,则OE=OF,但EF与BD不一定相等,所以不能判定四边形BFDE是正方形,本选项不符合题意;
B、若OE=OF,同样EF与BD不一定相等,所以不能判定四边形BFDE是正方形,本选项也不符合题意;
C、若∠EBD=45°,∵∠BOE=90°,∴∠BEO=45°,∴OE=OB,
∵AD=CD,∴∠DAE=∠DCF,又∵∠ADE=∠CDF,
∴△ADE≌△CDF(ASA),∴AE=CF,∴OE=OF,
∴EF=BD,∴四边形BFDE是正方形,本选项符合题意;
D、若∠DEF=∠BEF,由C选项的证明知OE=OF,但不能证明EF与BD相等,所以不能判定四边形BFDE是正方形,本选项不符合题意.
故选:C.

练习册系列答案
相关题目