题目内容
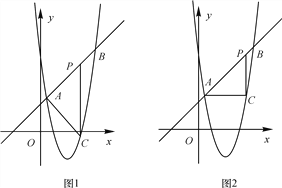
【题目】如图，直线y＝x＋2与抛物线y＝ax2＋bx＋6相交于A(
， 
)和B(4，m)，点P是线段AB上异于A、B的动点，过点P作PC⊥x轴，交抛物线于点C.
(1)求抛物线的表达式；
(2)是否存在这样的点P，使线段PC的长有最大值？若存在，求出这个最大值，若不存在，请说明理由；
(3)当△PAC为直角三角形时，求点P的坐标．
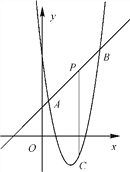
【答案】(1)y＝2x2－8x＋6(2)存在符合条件的点P(
， 
)，使线段PC的长有最大值
.(3)满足条件的点P有两个，为P1(3，5)，P2(
， 
)．
【解析】试题分析：（1）通过直线AB的解析式求出B点坐标。将点A和点B的坐标代入抛物线的解析式中得到一组关于a、b的二元一次方程组，解方程组求出a、b的值并代回抛物线的解析式中即可。
（2）根据直线AB的解析式设出点P的坐标。点P与点C的横坐标相同，由抛物线的解析式得出点C的坐标，即可得出PC关于点P坐标的表达式。根据二次函数的性质求出PC的长的最大值，即可求出点P的坐标。
（3）当△PAC是直角三角形时，有①∠PAC=90°和②∠PCA=90°这两种情况，分别求出这两种情况下的点P的坐标即可。
解：(1)∵B(4，m)在直线y＝x＋2上，
∴m＝6，B(4，6)．
∵A(
，
)、B(4，6)在抛物线y＝ax2＋bx＋6上，
∴
解得
∴所求抛物线的表达式为y＝2x2－8x＋6.
(2)设动点P的坐标为(n，n＋2)，则点C的坐标为(n，2n2－8n＋6)．
∴PC＝(n＋2)－(2n2－8n＋6)＝－2n2＋9n－4＝－2(n－
)2＋
.∵a＝－2＜0，
∴当n＝时，线段PC取得最大值，此时，P(，
)．
综上所述，存在符合条件的点P(，)，使线段PC的长有最大值.
(3)显然，∠APC≠90°，如图1，当∠PAC＝90°时，设直线AC的表达式为y＝－x＋b，把A(，)代入，得－＋b＝.解得b＝3.由－x＋3＝2x2－8x＋6，得x1＝3或x2＝ (舍去)．
当x＝3时，x＋2＝3＋2＝5.此时，点P的坐标为P1(3，5)．
如图2，当∠PCA＝90°时，由A(，)知，点C的纵坐标为y＝.
由2x2－8x＋6＝，得x1＝ (舍去)，x2＝
.当x＝时，x＋2＝＋2＝
.
此时，点P的坐标为P2(，)．
综上可知，满足条件的点P有两个，为P1(3，5)，P2(，)．
