题目内容
已知一次函数y=kx+b的图象经过点(﹣1,﹣5),且与正比例函数![]() 的图象相交于点(2,a).
的图象相交于点(2,a).
(1)求a的值.
(2)求一次函数y=kx+b的表达式.
(3)在同一坐标系中,画出这两个函数的图象.
考点:
待定系数法求一次函数解析式;一次函数的图象.
专题:
作图题;待定系数法.
分析:
(1)将点(2,a)代入正比例函数![]() 求出a的值.
求出a的值.
(2)根据(1)所求,及已知可知一次函数y=kx+b的图象经过两点(﹣1,﹣5)、(2,1),用待定系数法可求出函数关系式.
(3)由于一次函数与正比例函数的图象是一条直线,所以只需根据函数的解析式求出任意两点的坐标,然后经过这两点画直线即可.
解答:
解:(1)∵正比例函数![]() 的图象过点(2,a)
的图象过点(2,a)
∴a=1.(2)∵一次函数y=kx+b的图象经过两点(﹣1,﹣5)、(2,1)
∴![]() ,解得
,解得![]()
∴y=2x﹣3.
故所求一次函数的解析式为y=2x﹣3.(3)函数图象如图:
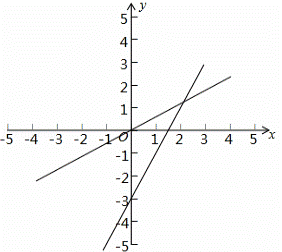
点评:
本题要注意利用正比例函数与一次函数的特点,来列出方程(组),求出未知数,写出解析式.

练习册系列答案
相关题目
 已知一次函数y=kx+2的图象经过A(-1,1).
已知一次函数y=kx+2的图象经过A(-1,1). m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.
m≠0)的图象相交于点 A(1,3)、B(n,-1)两点.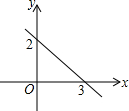 已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.
已知一次函数y=kx+b的图象如图所示,指出k、b的符号,并求出k和b的值.