题目内容
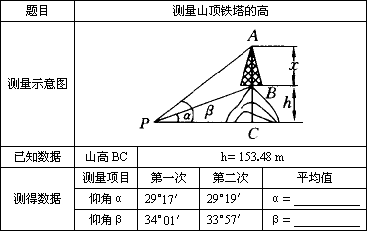
已知小山的高为h,为了测得小山顶上铁塔AB的高x,在平地上选择一点P,在P点处测得B点的仰角为α,A点的仰角为β,(见表中测量目标图)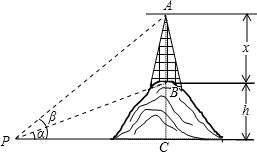
(1)试用α、β和h的关系式表示铁塔高x;
(2)在右表中根据第一次和第二次的“测得数据”,填写“平均值”一列中α、β的数值
(3)根据表中数据求出铁塔高x的值(精确到0.01m)
| 题目 | 测量山顶铁塔的高 | |||
| 测 量 目 标 |
||||
| 已知 数据 |
山高BC | h=153.48 | ||
| 测 得 数 据 |
测量项目 | 第一次 | 第二次 | 平均值 |
| 仰角α | 29°17′ | 29°19′ | α= | |
| 仰角β | 34°01′ | 33°57′ | β= | |
分析:(1)先根据锐角三角函数的定义用α、h表示出AC的长,再根据x+h=PC•tanβ即可求出答案;
(2)根据表中的测量数据求出α、β的平均值即可;
(3)把表中测量数据代入(1)中所求关系式即可.
(2)根据表中的测量数据求出α、β的平均值即可;
(3)把表中测量数据代入(1)中所求关系式即可.
解答:解:(1)由题意可知,BC=h,在Rt△BCP中,
PC=
=
;
同理,在Rt△APC中,AC=PC•tanβ=
•tanβ,
故x=
•tanβ-h;
(2)∵仰角α两次测得度数分别是:29°17′,29°19′,
∴α的平均值为:
=29°18′;
∵仰角β两次测得度数分别是:34°01′,33°57′,
∴β的平均值为:
=33°59′;
(3)由(1)可知,x=
•tanβ-h
≈
×0.6745-153.48
≈33.28(米).
答:塔高为33.28米.
PC=
| BC |
| tanα |
| h |
| tanα |
同理,在Rt△APC中,AC=PC•tanβ=
| h |
| tanα |
故x=
| h |
| tanα |
(2)∵仰角α两次测得度数分别是:29°17′,29°19′,
∴α的平均值为:
| 29°17′+29°19′ |
| 2 |
∵仰角β两次测得度数分别是:34°01′,33°57′,
∴β的平均值为:
| 34°01′+33°57′ |
| 2 |
(3)由(1)可知,x=
| h |
| tanα |
≈
| 153.48 |
| 0.5543 |
≈33.28(米).
答:塔高为33.28米.
点评:本题考查的是解直角三角形-仰角俯角问题,熟知锐角三角函数的定义是解答此题的关键.

练习册系列答案
相关题目
已知小山的高为h,为了测得小山顶上铁塔AB的高x,在平地上选择一点P,在P点处测得B点的仰角为α,A点的仰角为β,(见表中测量目标图)
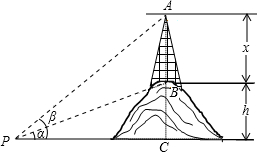
(1)试用α、β和h的关系式表示铁塔高x;
(2)在右表中根据第一次和第二次的“测得数据”,填写“平均值”一列中α、β的数值
(3)根据表中数据求出铁塔高x的值(精确到0.01m)
| 题目 | 测量山顶铁塔的高 | |||
| 测 量 目 标 | ||||
| 已知 数据 | 山高BC | h=153.48 | ||
| 测 得 数 据 | 测量项目 | 第一次 | 第二次 | 平均值 |
| 仰角α | 29°17′ | 29°19′ | α=______ | |
| 仰角β | 34°01′ | 33°57′ | β=______ | |
已知小山的高为h,为了测得小山顶上铁塔AB的高x,在平地上选择一点P,在P点处测得B点的仰角为α,A点的仰角为β,(见表中测量目标图)
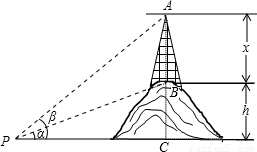
(1)试用α、β和h的关系式表示铁塔高x;
(2)在右表中根据第一次和第二次的“测得数据”,填写“平均值”一列中α、β的数值
(3)根据表中数据求出铁塔高x的值(精确到0.01m)

(1)试用α、β和h的关系式表示铁塔高x;
(2)在右表中根据第一次和第二次的“测得数据”,填写“平均值”一列中α、β的数值
(3)根据表中数据求出铁塔高x的值(精确到0.01m)
| 题目 | 测量山顶铁塔的高 | |||
| 测 量 目 标 | ||||
| 已知 数据 | 山高BC | h=153.48 | ||
| 测 得 数 据 | 测量项目 | 第一次 | 第二次 | 平均值 |
| 仰角α | 29°17′ | 29°19′ | α=______ | |
| 仰角β | 34°01′ | 33°57′ | β=______ | |