题目内容
 如图,AD=AE,AB=AC,∠A=60°,∠C=25°,则∠DOB=________度.
如图,AD=AE,AB=AC,∠A=60°,∠C=25°,则∠DOB=________度.
80
分析:先根据题目中所给条件证明△ABE≌△ACD,可得∠B=∠C=25°,也可求出∠ADC的度数,然后根据三角形的外角性质即可求得∠DOB的度数.
解答:在△ABE和△ACD中,
 ,
,
∴△ABE≌△ACD(SAS),
∴∠B=∠C=25°,
∵∠A=60°,
∴∠ADC=180°-∠A-∠C=105°,
∵∠ADC=∠DOB+∠B,
则∠DOB=105°-25°=80°.
故答案为:80.
点评:本题考查了全等三角形的判定与性质以及三角形的外角性质,解答本题的关键是掌握全等三角形的判定方法,以及全等三角形的性质:对应角相等.
分析:先根据题目中所给条件证明△ABE≌△ACD,可得∠B=∠C=25°,也可求出∠ADC的度数,然后根据三角形的外角性质即可求得∠DOB的度数.
解答:在△ABE和△ACD中,
 ,
,∴△ABE≌△ACD(SAS),
∴∠B=∠C=25°,
∵∠A=60°,
∴∠ADC=180°-∠A-∠C=105°,
∵∠ADC=∠DOB+∠B,
则∠DOB=105°-25°=80°.
故答案为:80.
点评:本题考查了全等三角形的判定与性质以及三角形的外角性质,解答本题的关键是掌握全等三角形的判定方法,以及全等三角形的性质:对应角相等.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
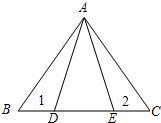 2、如图,AD=AE,∠1=∠2,BD=CE,则有△ABD≌△
2、如图,AD=AE,∠1=∠2,BD=CE,则有△ABD≌△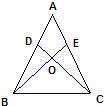 21、已知:如图,AD=AE,∠ADC=∠AEB,BE与CD相交于O点.
21、已知:如图,AD=AE,∠ADC=∠AEB,BE与CD相交于O点.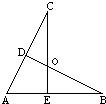 39、已知:如图,AD=AE,AB=AC,BD、CE相交于O.
39、已知:如图,AD=AE,AB=AC,BD、CE相交于O.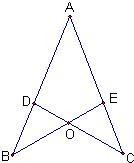 23、已知:如图,AD=AE,AB=AC,DC与BE交于O点.
23、已知:如图,AD=AE,AB=AC,DC与BE交于O点.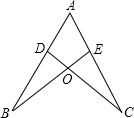 如图,AD=AE,AB=AC,∠A=60°,∠C=25°,则∠DOB=
如图,AD=AE,AB=AC,∠A=60°,∠C=25°,则∠DOB=