题目内容
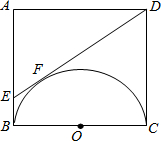如图，以正方形ABCD的边BC为直径作半圆O，过点D作直线切半圆于点F，交AB于点E，则△DAE与直角梯形EBCD的周长的比值为
- A.
- B.
- C.
- D.
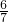
D
分析：EF=x，DF=y，在△ADE中根据勾股定理可得列方程，从而得到三角形ADE的周长和直角梯形EBCD周长，从而可求得两者周长之比．
解答：根据切线长定理得，BE=EF，DF=DC=AD=AB=BC．
设EF=x，DF=y，
∵（y-x）2+y2=（x+y）2，
∴y=4x，
∴三角形ADE的周长为12x，直角梯形EBCD周长为14x，
∴两者周长之比为12x：14x=6：7．
故选D．
点评：此题考查圆的切线长定理，正方形的性质和勾股定理等知识，解答本题关键是运用切线长定理得出EB=EF，DF=DC，从而求解．
分析：EF=x，DF=y，在△ADE中根据勾股定理可得列方程，从而得到三角形ADE的周长和直角梯形EBCD周长，从而可求得两者周长之比．
解答：根据切线长定理得，BE=EF，DF=DC=AD=AB=BC．
设EF=x，DF=y，
∵（y-x）2+y2=（x+y）2，
∴y=4x，
∴三角形ADE的周长为12x，直角梯形EBCD周长为14x，
∴两者周长之比为12x：14x=6：7．
故选D．
点评：此题考查圆的切线长定理，正方形的性质和勾股定理等知识，解答本题关键是运用切线长定理得出EB=EF，DF=DC，从而求解．
练习册系列答案
相关题目
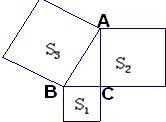13、如图，以直角△ABC的三边向外作正方形，其面积分别为S1，S2，S3且S1=4，S2=8，则S3=
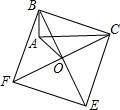如图，以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF，设正方形的中心为O，连接AO，如果AB=4，AO=6
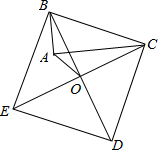如图，以Rt△ABC的斜边BC为一边作正方形BCDE，设正方形的中心为O，连接AO，如果AB=3，AO=
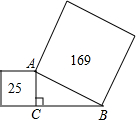如图，以Rt△ABC的斜边和一直角边为边长向外作正方形，面积分别为169和25，则另一直角边的长度BC为（ ）
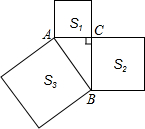如图，以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3，且S1+S2+S3=50，则AB=（ ）